当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
3052:Geodes
Special Judge 特殊评判题目描述
In the mountains of Geodesia, geodes are found. These 'hollow' stones contain cavities with crystal formations around them. The beautifully colored crystals can be sold for a high price to people both inside and outside of Geodesia. The problem with geodes is that one cannot see from the outside of a given rock whether it is a geode or not. Out of every thousand rocks found in Geodesia only some are geodes.
In order to find out whether a given rock is in fact a geode, one can try to consider its density
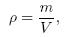
where m represents its mass and V its volume. Since a geode contains empty space, a rock contaning one is expected to have a lower density than other rocks. If the density of a rock is too high, it would be a waste of time and effort to further investigate it.
But how could one determine the density of each of the enormous number of rocks found in the mountains of Geodesia? Minig crafts collect rocks, which they put on mobile conveyer belts. Weighing the rocks automatically at a fast rate is no problem, but how to quickly determine their volume? Measuring e.g. the volume displacement of a liquid(like H2O), where each rock has to be put in and taken out individually is a time consuming process.
So why not try to estimate the volume just by looking at the rock? Along the conveyer belt, two cameras are placed, perpendicular to each other. Of every rock that passes, they each take a picture. These pictures are sent to a computer for processing. The computer calculates from these pictures an upper bound for the volume of the rock, Vmax. A lower bound for the density of the rock is then given by
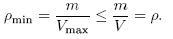
This lower bound can then be used to reject rocks that are certainly too heavy to be geodes.
The computer uses a relatively simple trick for estimating the maximal volume. It considers the picures taken as silhouettes, as parallel projections of a rock onto a planes. Since the two cameras are placed perpendicular to each other, the projection planes are also perpendicular to each other.
In other words, choose a coordinate system in three dimensional space as follows: z runs along the vertical direction and x and y run along the perpendicular horizontal directions in which the two cameras are placed. Let S ∈ R3 represent a rock. Then the cameras yield the two parallel projections
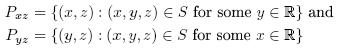
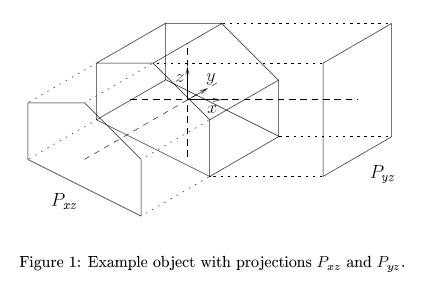
on the xz and yz plane respectively. See Figure 1 for an example.
Now a curious property of the rocks found in Geodesia makes the measurement of the volume easier: they are all convex1. Furthermore, the projections can be considered as polygons. So first each of the two pictures taken of a rock is converted into a convex polygon by an image recognition program. You are to write a program that will do the second step: compute from these two polygons Vmax: the maximum volume of any rock having exactly these two polygon-shaped projections.
In order to find out whether a given rock is in fact a geode, one can try to consider its density
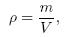
where m represents its mass and V its volume. Since a geode contains empty space, a rock contaning one is expected to have a lower density than other rocks. If the density of a rock is too high, it would be a waste of time and effort to further investigate it.
But how could one determine the density of each of the enormous number of rocks found in the mountains of Geodesia? Minig crafts collect rocks, which they put on mobile conveyer belts. Weighing the rocks automatically at a fast rate is no problem, but how to quickly determine their volume? Measuring e.g. the volume displacement of a liquid(like H2O), where each rock has to be put in and taken out individually is a time consuming process.
So why not try to estimate the volume just by looking at the rock? Along the conveyer belt, two cameras are placed, perpendicular to each other. Of every rock that passes, they each take a picture. These pictures are sent to a computer for processing. The computer calculates from these pictures an upper bound for the volume of the rock, Vmax. A lower bound for the density of the rock is then given by
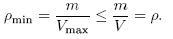
This lower bound can then be used to reject rocks that are certainly too heavy to be geodes.
The computer uses a relatively simple trick for estimating the maximal volume. It considers the picures taken as silhouettes, as parallel projections of a rock onto a planes. Since the two cameras are placed perpendicular to each other, the projection planes are also perpendicular to each other.
In other words, choose a coordinate system in three dimensional space as follows: z runs along the vertical direction and x and y run along the perpendicular horizontal directions in which the two cameras are placed. Let S ∈ R3 represent a rock. Then the cameras yield the two parallel projections
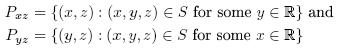
on the xz and yz plane respectively. See Figure 1 for an example.
Now a curious property of the rocks found in Geodesia makes the measurement of the volume easier: they are all convex1. Furthermore, the projections can be considered as polygons. So first each of the two pictures taken of a rock is converted into a convex polygon by an image recognition program. You are to write a program that will do the second step: compute from these two polygons Vmax: the maximum volume of any rock having exactly these two polygon-shaped projections.
输入解释
The first line of input contains a single number:the number of test cases to follow. Each test case has the following format:

- One line with the integer nxz the number of vertices describing the projection on the xz plane.
- nxz lines, each with two integers x and z, separated by a single space: the coordinates of one vertex of the xz projection.
- One line with the integer nyz, the number of vertices describing the projection on the yz plane.
- nyz lines, each with two integers y and z, seperated by a single space: the coordinates of one vertex of the yz projection.
输出解释
For every test case in the input, the output should contain a single number on a single line: Vmax, the maximum volume of any object having the projections given in the input, rounded in the usual way to two decimals behind the decimal point, A round-off error of 0.01 is permitted in your answer.
输入样例
1 5 1 0 1 -1 -1 0 -1 1 0 1 5 -1 1 0 1 1 1 1 -1 -1 -1
输出样例
5.00
提示
1.A set S(in R2, R3, or in fact in any vector space you like) is convex if any straight line segment connecting any two points a, b ∈ S is again completely within S. Formally this means that for all a,b ∈ S and all x ∈ [0, 1], also xa + (1-x)b ∈ S.
最后修改于 2020-10-29T06:51:13+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 1000 | 65536 |
登陆或注册以提交代码