当前你的浏览器版本过低，网站已在兼容模式下运行，兼容模式仅提供最小功能支持，网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
2746：Bingo
题目描述
A Bingo game is played by one gamemaster and several players. At the beginning of a game, each player is given a card with M *M numbers in a matrix (See Figure 10).
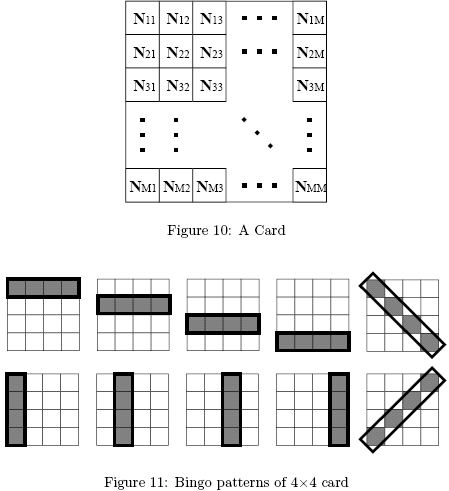
As the game proceeds, the gamemaster announces a series of numbers one by one. Each player punches a hole in his card on the announced number, if any.
When at least one 'Bingo' is made on the card, the player wins and leaves the game. The 'Bingo' means that all the M numbers in a line are punched vertically, horizontally or diagonally (See Figure 11).
The gamemaster continues announcing numbers until all the players make a Bingo.
In the ordinary Bingo games, the gamemaster chooses numbers by a random process and has no control on them. But in this problem the gamemaster knows all the cards at the beginning of the game and controls the game by choosing the number sequence to be announced at his will.
Specifically, he controls the game to satisfy the following condition.
Figure 12 shows an example of how a game proceeds. The gamemaster cannot announce '5' before '16', because Card4 makes a Bingo before Card2 and Card3, violating the condition (*).
Your job is to write a program which finds the minimum length of such sequence of numbers for the given cards.
As the game proceeds, the gamemaster announces a series of numbers one by one. Each player punches a hole in his card on the announced number, if any.
When at least one 'Bingo' is made on the card, the player wins and leaves the game. The 'Bingo' means that all the M numbers in a line are punched vertically, horizontally or diagonally (See Figure 11).
The gamemaster continues announcing numbers until all the players make a Bingo.
In the ordinary Bingo games, the gamemaster chooses numbers by a random process and has no control on them. But in this problem the gamemaster knows all the cards at the beginning of the game and controls the game by choosing the number sequence to be announced at his will.
Specifically, he controls the game to satisfy the following condition.
- Cardi makes a Bingo no later than Cardj, for i < j. (*)
Figure 12 shows an example of how a game proceeds. The gamemaster cannot announce '5' before '16', because Card4 makes a Bingo before Card2 and Card3, violating the condition (*).
Your job is to write a program which finds the minimum length of such sequence of numbers for the given cards.
输入解释
The input consists of multiple datasets. The format of each dataset is as follows.
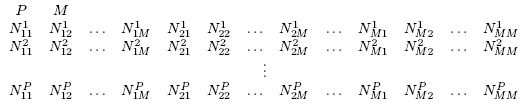
All data items are integers. P is the number of the cards, namely the number of the players. M is the number of rows and the number of columns of the matrix on each card. Nkij means the number written at the position (i, j) on the k-th card. If (i, j) != (p, q), then Nkij != Nkpq. The parameters P, M, and N satisfy the conditions 2 <= P <= 4, 3 <= M <= 4, and 0 <= Nkij <= 99.
The end of the input is indicated by a line containing two zeros separated by a space. It is not a dataset.
All data items are integers. P is the number of the cards, namely the number of the players. M is the number of rows and the number of columns of the matrix on each card. Nkij means the number written at the position (i, j) on the k-th card. If (i, j) != (p, q), then Nkij != Nkpq. The parameters P, M, and N satisfy the conditions 2 <= P <= 4, 3 <= M <= 4, and 0 <= Nkij <= 99.
The end of the input is indicated by a line containing two zeros separated by a space. It is not a dataset.
输出解释
For each dataset, output the minimum length of the sequence of numbers which satisfy the condition (*). Output a zero if there are no such sequences. Output for each dataset must be printed on a separate line.
输入样例
4 3 10 25 11 20 6 2 1 15 23 5 21 3 12 23 17 7 26 2 8 18 4 22 13 27 16 5 11 19 9 24 2 11 5 14 28 16 4 3 12 13 20 24 28 32 15 16 17 12 13 21 25 29 33 16 17 18 12 13 22 26 30 34 17 18 15 12 13 23 27 31 35 18 15 16 4 3 11 12 13 14 15 16 17 18 19 21 22 23 24 25 26 27 28 29 31 32 33 34 35 36 37 38 39 41 42 43 44 45 46 47 48 49 4 4 2 6 9 21 15 23 17 31 33 12 25 4 8 24 13 36 22 18 27 26 35 28 3 7 11 20 38 16 5 32 14 29 26 7 16 29 27 3 38 14 18 28 20 32 22 35 11 5 36 13 24 8 4 25 12 33 31 17 23 15 21 9 6 2 0 0
输出样例
5 4 12 0
提示
For your convenience, sequences satisfying the condition (*) for the first three datasets are shown below. There may be other sequences of the same length satisfying the condition, but no shorter.
11, 2, 23, 16, 5
15, 16, 17, 18
11, 12, 13, 21, 22, 23, 31, 32, 33, 41, 42, 43
11, 2, 23, 16, 5
15, 16, 17, 18
11, 12, 13, 21, 22, 23, 31, 32, 33, 41, 42, 43
最后修改于 2020-10-29T06:41:25+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 5000 | 65536 |
登陆或注册以提交代码