2428：Surface Reconstruction

(3-D) medical imaging devices, such as CT and MRI, typically produce images as a set of slices. From these slices of images we can reconstruct the surface of the object. People have done much research on this field, and a classical method to simplify the problem is to just consider the surface reconstruction problem between two adjacent slices.

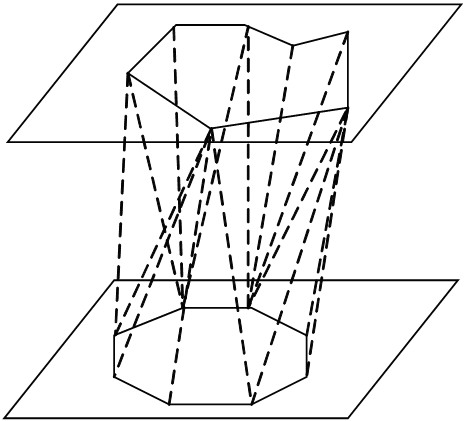
We describe the problem as: given two simple polygons (a simple polygon is a polygon from which we cannot find two boundaries which are intersectant and not adjacent) in two parallel plane, then we can connect segments between the points from different polygons, and form some triangles; these triangles may construct a close side surface of two polygons (as show in the figure above). We can easily find that the triangles must obey the following properties: a boundary of the polygons must belong to one and just one triangle; a triangle must include one and just one boundary of the polygons.

For two simple polygons that are given in two parallel planes, there are a lot of ways to connect the segments, and different ways may look different. There is also much research in this problem, but to make it simple, your job is just to calculate a way of connecting such that the area of the side surface is minimum.

The first line contains an integer P (3 <= P <= 100), which is the number of points in the first polygon. The second line contains P pairs of integers, which give the coordinates of the P points in turn.

The third line contains an integer Q (3 <= Q <= 100), which is the number of points in the second polygon. The fourth line contains Q pairs of integers, which give the coordinates of the Q points in turn.

It is known that the distance between two planes is 10, and all the coordinates given above are in the range of [0, 2500].

The output contains only one line, which gives the minimum area of the close side surface. The result should be round to an integer.