当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
1341:The Strongest Subchains
题目描述
Let A be an array of N , 1 < N <= 50000 and N is even, integers.We use A[i] to denote the ith element of the array.Hence the array contains elements A[0], A[1] ? ? ? A[N − 1]. Each element of A is a nonnegative integer in the range of 0 through 9972. Given two integers x and y, let (x mod y) be the integer that is the remainder of y dividing x. It happens that A[i] = (a1*i *i + a2*i + a3) mod 9973 for some integers a1, a2, and a3. We know 1 <= ai <= 50000 for i = 1, 2, 3. For example, if N = 6, a1= 1, a2= 1, and a3= 1, then we have the following:
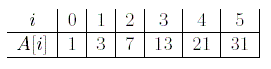
There are three additional arrays S, E and R. Each of the three arrays has M , 1 <= M <= 50000, integers. We know 1 <= S[i] <= E[i] <= N . It happens that S[i] = (s1*i*i+ s2*i + s3) mod (N/2) and E[i] = S[i] + [(e1*i*i+ e2*i + e3) mod (N/2)]. Assume 1 <= si, ei<= 50000 for i = 1, 2, 3. We also know R[i] = min{A[S[i]], A[S[i] + 1], ... , A[E[i]]} for each i where 0 <= i <= M − 1. Your task is to find the smallest j such that R[j] = max{R[0], R[1], ... , R[M − 1]}. For example, if A is given as the above example, M = 3, s1= 1, s2= 1, s3= 1, e1= 1, e2= 1, and e3= 1, then we have the following:
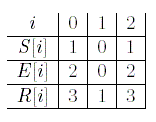
Hence max{R[0], R[1], R[2]} = 3 and R[0] has the smallest index with its value equaling 3. Thus we output 0.
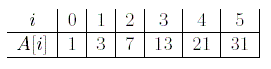
There are three additional arrays S, E and R. Each of the three arrays has M , 1 <= M <= 50000, integers. We know 1 <= S[i] <= E[i] <= N . It happens that S[i] = (s1*i*i+ s2*i + s3) mod (N/2) and E[i] = S[i] + [(e1*i*i+ e2*i + e3) mod (N/2)]. Assume 1 <= si, ei<= 50000 for i = 1, 2, 3. We also know R[i] = min{A[S[i]], A[S[i] + 1], ... , A[E[i]]} for each i where 0 <= i <= M − 1. Your task is to find the smallest j such that R[j] = max{R[0], R[1], ... , R[M − 1]}. For example, if A is given as the above example, M = 3, s1= 1, s2= 1, s3= 1, e1= 1, e2= 1, and e3= 1, then we have the following:

Hence max{R[0], R[1], R[2]} = 3 and R[0] has the smallest index with its value equaling 3. Thus we output 0.
输入解释
The first line contains the number of test cases w. Then the w test cases are listed one by one. Each test case is listed as follows in one line with a space between two integers: N , a1, a2, a3, M ,s1, s2, s3, e1, e2, e3.
输出解释
For each test case, output the smallest value j such that R[j] = max{R[0], R[1], R[2], . . . , R[M − 1]} in one line.
输入样例
1 6 1 1 1 3 1 1 1 1 1 1
输出样例
0
最后修改于 2020-10-29T06:01:22+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 1000 | 10000 |
登陆或注册以提交代码