1340：The Longest Detour Problem

Let G be a weighted graph, i.e., every edge in G is associated with a nonnegative integer weight. The length of a path is the sum of edge weights in the path. A shortest path between vertices r and s in G, denoted by P_G(r, s), is defined as a path with the shortest length from r to s. The distance between vertices r and s, denoted by d_G(r, s), is the length of the shortest path P_G(r, s). For two vertices in a connected graph, there exists at least one shortest path between them. Let e = (u, v) be an edge in P_G(r, s) with v closer to s than u (v may be s). Let G - e denote the subgraph obtained by removing edge e from G. A detour from u is the shortest path from u to s in G - e, or P_G-e(u, s). Edge e is a detour -critical edge in P_G(r, s) if the removal of e results in the maximum distance increment from u to s. In other words, if e is a detour -critical edge in P_G(r, s), then d_G-e(u, s) - d_G(u, s) is maximum among all edges in P_G(r, s). The longest detour problem is to find the maximum distance increment of a shortest path.



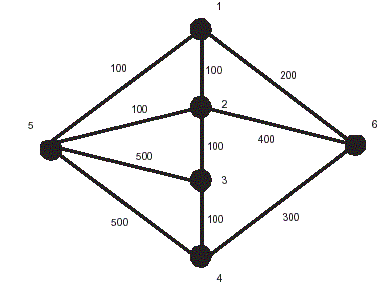
Figure 4: A weighted graph G.

For example, see Figure 4. P_G(4, 1) =< 4, 3, 2, 1 > is the shortest path from vertex 4 to vertex 1. Path < 4, 6, 1 > is the detour from vertex 4 to vertex 1 if edge (4, 3) is removed. Path < 3, 5, 1 > is the detour from vertex 3 to vertex 1 if edge (3, 2) is removed. Path < 2, 5, 1 > is the detour from vertex 2 to vertex 1 if edge (2, 1) is removed. The detour -critical edge in P_G(4, 1) is not edge (4, 3) or edge (2, 1) but edge (3, 2) since d_G-(3,2)(3, 1) - d_G(3, 1) = 600 - 200 = 400 is greater than d_G-(4,3)(4, 1) - d_G(4, 1) = 500 - 300 = 200 and d_G-(2,1)(2, 1) - d_G(2, 1) = 200 - 100 = 100.

The algorithm for finding detours, as well as determining the detour-critical edges, is important from the viewpoint of network management. Due to a sudden edge failure

from some vertex, the message must be retransmitted through a detour from the vertex adjacent to the faulty edge.

Suppose that we have several networks. Each network is connected and contains at most n vertices, where 3 <= n <= 100. Assume now that you are hired to serve as a

network administrator and have to determine the maximum distance increment caused by a detour-critical edge of a given shortest path for each network.

The input consists of several test cases. The first line contains an integer indicating the number of test cases. Each test case starts with a positive integer n, where 3 <= n <= 100. The following n lines represent the adjacency matrix of a network. An adjacency matrix of a network G with n vertices, denoted by A(G) = [w_u,v], is an n * n matrix such that w_u,v > 0 if (u, v) is an edge of G, and w_u,v= 0 otherwise, where w_u,v in a nonnegative integer. Note that any two elements in each line of an adjacency matrix are separated by a space. The last line of each test case represents the sequence of vertices in a given shortest path in which there is also a space between two vertices. Note that the first and the last vertices denote the source and the destination vertices, respectively. For example, the adjacency matrix of the graph in Figure 4 is shown in test case 3 of the sample input.

For each test case, output the maximum distance increment caused by the detour-critical edge of the given shortest path in one line.