1339：poker card game

Suppose you are given many poker cards. As you have already known, each card has points ranging from 1 to 13. Using these poker cards, you need to play a game on the cardboard in Figure 1. The game begins with a place called START. From START, you can walk to left or right to a rectangular box. Each box is labeled with an integer, which is the distance to START.


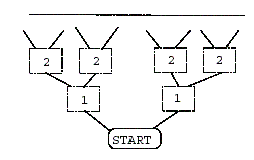
Figure 1: The poker card game cardboard.

To place poker cards on these boxes, you must follow the rules below: (1) If you put a card with n points on a box labeled i , you got (n ∗ i) points. (2) Once you place a card on a box b, you block the paths to the boxes behind b. For example, in Figure 2, a player places a queen on the right box of distance 1, he gets 1 ∗ 12 points but the queen also blocks the paths to boxes behind it; i.e., it is not allowed to put cards on boxes behind it anymore.



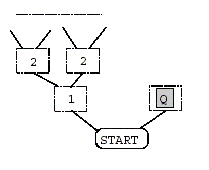
Figure 2: Placing a queen.

Your goal: Given a number of poker cards, find a way to place them so that you will get the minimum points. For example, suppose you have 3 cards 5, 10, and K. To get the minimum points, you can place cards like Figure 3, where the total points are 1 * 13 + 2 * 5 + 2 * 10 = 43.



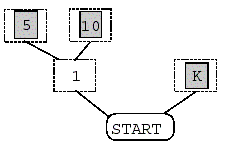
Figure 3: An example to place cards.

The first line of the input file contains an integer n, n <= 10, which represents the number of test cases. In each test case, it begins with an integer m, m <= 100000,

which represents the number of poker cards. Next, each card represented by its number are listed consecutively. Note that, the numbers of ace, 2, 3, ..., K are given by integers 1, 2, 3, ..., 13, respectively. The final minimum point in each test case is less than 5000000.

List the minimum points of each test case line by line.