当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
1191:棋盘分割
题目描述
将一个8*8的棋盘进行如下分割:将原棋盘割下一块矩形棋盘并使剩下部分也是矩形,再将剩下的部分继续如此分割,这样割了(n-1)次后,连同最后剩下的矩形棋盘共有n块矩形棋盘。(每次切割都只能沿着棋盘格子的边进行)
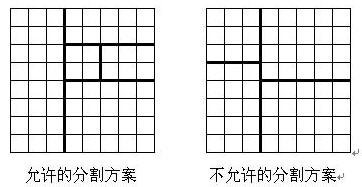
原棋盘上每一格有一个分值,一块矩形棋盘的总分为其所含各格分值之和。现在需要把棋盘按上述规则分割成n块矩形棋盘,并使各矩形棋盘总分的均方差最小。
均方差__poj_jax_start__\sigma=\sqrt{\frac{\sum_{i=1}^n(x_i-\bar{x})^2}{n}}__poj_jax_end__,其中平均值__poj_jax_start__\bar{x}=\frac{\sum_{i=1}^nx_i}{n}__poj_jax_end__,xi为第i块矩形棋盘的总分。
请编程对给出的棋盘及n,求出O'的最小值。

原棋盘上每一格有一个分值,一块矩形棋盘的总分为其所含各格分值之和。现在需要把棋盘按上述规则分割成n块矩形棋盘,并使各矩形棋盘总分的均方差最小。
均方差__poj_jax_start__\sigma=\sqrt{\frac{\sum_{i=1}^n(x_i-\bar{x})^2}{n}}__poj_jax_end__,其中平均值__poj_jax_start__\bar{x}=\frac{\sum_{i=1}^nx_i}{n}__poj_jax_end__,xi为第i块矩形棋盘的总分。
请编程对给出的棋盘及n,求出O'的最小值。
输入解释
第1行为一个整数n(1 < n < 15)。
第2行至第9行每行为8个小于100的非负整数,表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。
第2行至第9行每行为8个小于100的非负整数,表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。
输出解释
仅一个数,为O'(四舍五入精确到小数点后三位)。
输入样例
3 1 1 1 1 1 1 1 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 0 3
输出样例
1.633
最后修改于 2020-10-29T05:57:12+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 1000 | 10000 |
登陆或注册以提交代码