7245：Photos

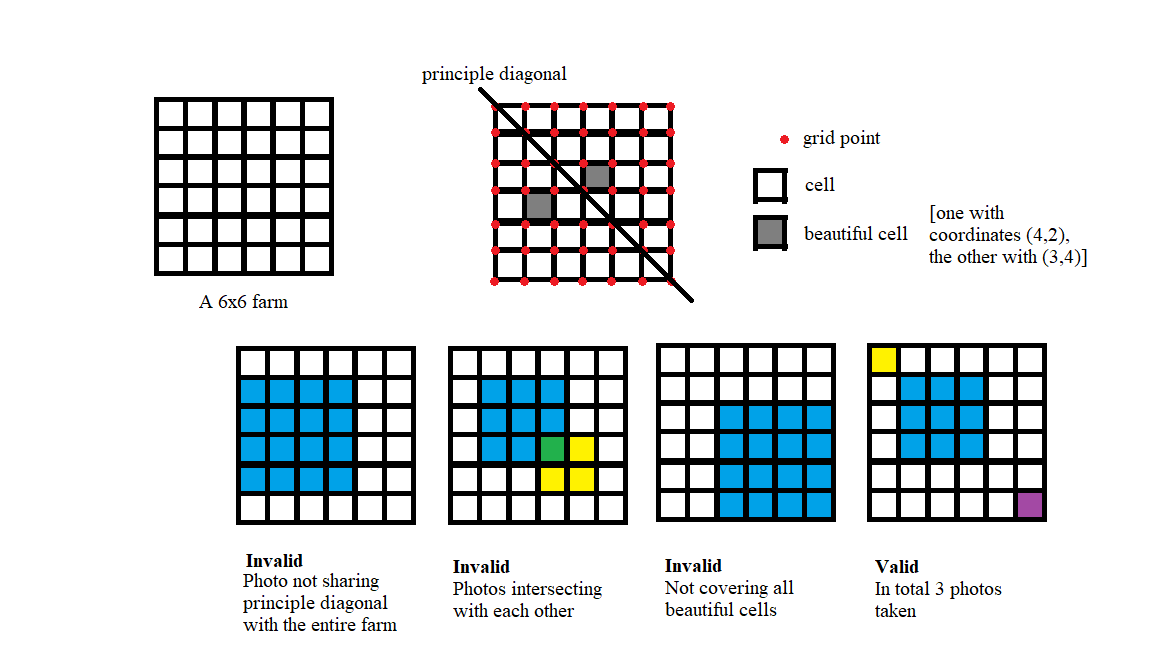
You have a square farm, divided into $n\times n$ cells. There are $m$ beautiful cells among all cells, whose locations are given. You would like to take some photos of the farm. A photo should figure a square area of the farm, with vertices located on grid points and edges parallel to the grid lines. What's more, its principal diagonal should lie on the principal diagonal of the whole farm.

You would like to take several photos so that each beautiful cell is contained in one photo. You hate repetitions so that any two of your photos should not coincide, that is, their common area is $0$. Each photo can contain an arbitrary number of beautiful cells, possibly $0$, $1$ or more. Count the number of set of photos satisfying the above conditions, modulo $998244353$.

In case you are confused, here we provide an illustration. The farm shown in this illustration is the same as the one in the sample test case.


You are given $T$ independent test cases; solve each of them.

The first line of input contains a single integer $T(1\leq T\leq 1500)$, indicating the number of test cases. Then $T$ test cases follow.

The first line of each test case contains two space-separated integers $n,m(1\leq n\leq 10^9,1\leq m\leq 10^5)$, denoting the size of the farm and the number of good cells. Each of the next $m$ lines contains two space-separated integers $x_i,y_i(1\leq x_i,y_i\leq n)$, denoting the coordinates of a good cell.

It is guaranteed that $\sum m\leq 10^6$.

For each test case, print a line consisting of a single integer, indicating the answer modulo $998244353$.