当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
6822:Paperfolding
题目描述
There is a piece of paper in rectangular shape with sufficient length and width (lay flat on the table). Execute an operation instruction according to a string of length $n$ from left to right that only contains $4$ different characters of $L$,$R$,$U$,$D$.
1. $L$ instruction means to fold it from left to right,
2. $R$ instruction means to fold from right to left,
3. $U$ instruction means to fold from top to bottom,
4. $D$ instruction means to fold in half from bottom to top.
Note that the operation is limited due to the limitation of the desktop. Namely, the fold operation is restricted. For example, if you fold the paper from left to right, you should let the left side overlap on the right side with no rotation.
Now, cut a knife horizontally (completely cut) at the center of the visible part of the paper, and then cut vertically (completely cut).
The number of pieces of the whole paper split is $num(S)$.
See the example and the picture for better understanding.
Now given a nonnegative integer $n$, the string $S$ is generated from $4^n$ different possible outcomes in equal probability. Find the expected value of the number of pieces of the paper which is split, that is $E(num(S))$ mod $998244353$.
It can be shown that the answers can be represented by $\frac{P}{Q}$, where $P$ and $Q$ are coprime integers, and print the value of $P \times Q^{-1} \ mod $ $\space 998244353$.
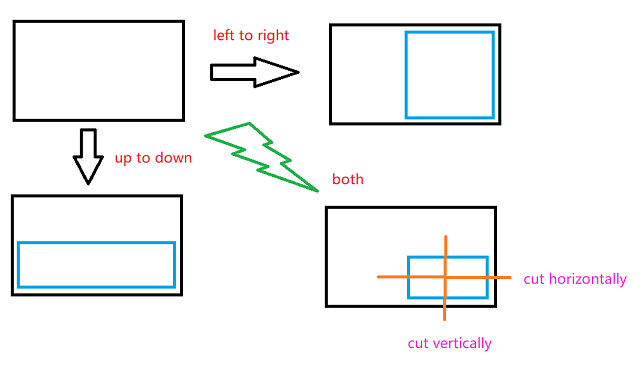
1. $L$ instruction means to fold it from left to right,
2. $R$ instruction means to fold from right to left,
3. $U$ instruction means to fold from top to bottom,
4. $D$ instruction means to fold in half from bottom to top.
Note that the operation is limited due to the limitation of the desktop. Namely, the fold operation is restricted. For example, if you fold the paper from left to right, you should let the left side overlap on the right side with no rotation.
Now, cut a knife horizontally (completely cut) at the center of the visible part of the paper, and then cut vertically (completely cut).
The number of pieces of the whole paper split is $num(S)$.
See the example and the picture for better understanding.
Now given a nonnegative integer $n$, the string $S$ is generated from $4^n$ different possible outcomes in equal probability. Find the expected value of the number of pieces of the paper which is split, that is $E(num(S))$ mod $998244353$.
It can be shown that the answers can be represented by $\frac{P}{Q}$, where $P$ and $Q$ are coprime integers, and print the value of $P \times Q^{-1} \ mod $ $\space 998244353$.

输入解释
The first line contains a single integer $ T $ ($1 \le T \le 10^5$), the number of testcases.
Each of the next $ T $ lines contains a number $ n $ ( $0 \le n \le 10^{18} $ ).
Each of the next $ T $ lines contains a number $ n $ ( $0 \le n \le 10^{18} $ ).
输出解释
For each testcase, print the answer in one line.
输入样例
2 0 1
输出样例
4 6
来自杭电HDUOJ的附加信息
| Recommend | IceyWang |
最后修改于 2020-10-25T23:34:41+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 2000/1000MS(Java/Others) | 131072/131072K(Java/Others) |
登陆或注册以提交代码