当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
2455:Dividing Sea Area to Navigation-Triangle
题目描述
When a vessel sails on the vast and boundless sea, the captain must know his position in any time. There is a technique called triangle-navigation can solves this problem.
Suppose there are three islands in some sea area. They form a large triangle. There is a radio navigation station respectively on each island. The navigation station sends out radio signals continuously. After the vessel receives the signals, its position can be known by calculating those three different signals.
There is a raised n-multilateral sea area which is formed by n islands. Each island has a radio navigation station. The n islands form a raised n-multilateral graph. Every three islands form a triangle division area. Vessels sailing in this triangle area should determine the position by the signals from those three radio navigation stations in the three islands.
Of course, all navigation triangles divided from the raised n-multilateral graph can not overlap one another. Consequently, this raised n-multilateral graph is divided into n-2 triangles areas.
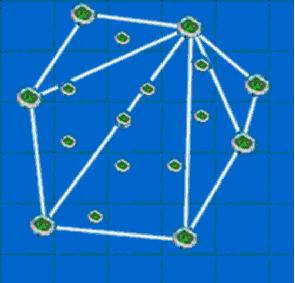
By the way, there are some smaller islets in the raised n-multilateral sea area and there is no navigation station in any islet. These small islets are related with our problem, we will explain it later.
An experienced captain had navigated in this sea area for several years. However, he found it is improper to divide the sea area to n-2 navigation triangles as the current scheme. After deep thinking, he put forward a new method.
Of course, he still divided raised n-multilateral graph sea area into n-2 navigation triangles which are not overlapped one another. The three vertexes of the triangles are three islands with navigation station. According to the scheme which is put forward by the old captain, a weight value is necessary for each triangle sea division area. Calculating formula of the weight value is as follows:
V= S+2*a +b
In that formula, the letter “V” expresses the weight value of the triangle sea area, the letter “S” expresses the area of that triangle sea, The letter “a” expresses the number of smaller islets inside the triangle. The letter “b” expresses the number of those small islets on the common edge between the two triangle sea areas. After calculating according to the formula above, each triangle sea area division has a weight value. The old captain thought, for the n-2 triangle areas, there will be n-2 weight values. Among these weight values, when the difference of the maximum weight value and the minimum weight value reaches a minimum, this scheme of division is optimum. That scheme will benefit sailing most.
As none people can solve that problem on the vessel. Now the captain is visiting you, he hopes you can help him.
Suppose there are three islands in some sea area. They form a large triangle. There is a radio navigation station respectively on each island. The navigation station sends out radio signals continuously. After the vessel receives the signals, its position can be known by calculating those three different signals.
There is a raised n-multilateral sea area which is formed by n islands. Each island has a radio navigation station. The n islands form a raised n-multilateral graph. Every three islands form a triangle division area. Vessels sailing in this triangle area should determine the position by the signals from those three radio navigation stations in the three islands.
Of course, all navigation triangles divided from the raised n-multilateral graph can not overlap one another. Consequently, this raised n-multilateral graph is divided into n-2 triangles areas.

By the way, there are some smaller islets in the raised n-multilateral sea area and there is no navigation station in any islet. These small islets are related with our problem, we will explain it later.
An experienced captain had navigated in this sea area for several years. However, he found it is improper to divide the sea area to n-2 navigation triangles as the current scheme. After deep thinking, he put forward a new method.
Of course, he still divided raised n-multilateral graph sea area into n-2 navigation triangles which are not overlapped one another. The three vertexes of the triangles are three islands with navigation station. According to the scheme which is put forward by the old captain, a weight value is necessary for each triangle sea division area. Calculating formula of the weight value is as follows:
V= S+2*a +b
In that formula, the letter “V” expresses the weight value of the triangle sea area, the letter “S” expresses the area of that triangle sea, The letter “a” expresses the number of smaller islets inside the triangle. The letter “b” expresses the number of those small islets on the common edge between the two triangle sea areas. After calculating according to the formula above, each triangle sea area division has a weight value. The old captain thought, for the n-2 triangle areas, there will be n-2 weight values. Among these weight values, when the difference of the maximum weight value and the minimum weight value reaches a minimum, this scheme of division is optimum. That scheme will benefit sailing most.
As none people can solve that problem on the vessel. Now the captain is visiting you, he hopes you can help him.
输入解释
Two positive integers n (3<=n <=100) and m (0 <=m<=20) are provided firstly in each test case. They take up one line respectively, then n lines of data follow, there are 2 floating numbers in each line expressing coordinates of radio navigation station, then following m lines, there are 2 floating numbers in every line expressing coordinates of smaller islets which are not equipped with radio navigation station. Input is terminated by end of file.
输出解释
For each case, when the difference of weight value between the maximum weight value and minimum weight value is minimum, output this difference, the result should be a floating-point-number, having 2 digits after radix point.
输入样例
4 2 0 0 1 0 1 1 0 1 0.2 0.2 0.5 0.9 4 10 0 0 1 0 1 1 0 1 0.5 0.1 0.5 0.2 0.5 0.3 0.5 0.4 0.5 0.5 0.5 0.6 0.5 0.7 0.5 0.8 0.5 0.9 0.2 0.1
输出样例
0.00 2.00
来自杭电HDUOJ的附加信息
| Recommend | gaojie |
最后修改于 2020-10-25T22:53:36+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 5000/1000MS(Java/Others) | 32768/32768K(Java/Others) |
登陆或注册以提交代码