当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
1842:Gorilla.bas
题目描述
Maybe you remember the old QBasic game gorilla.bas. But in case you don’t, the game was about two gorillas who were throwing explosive bananas at each other. Each gorilla was controlled by one of the two players. Each player could choose the angle and speed of the shot and the banana would follow a parabolic trajectory. As if finding the appropriate angle and speed in order to hit the opponent’s gorilla wasn’t difficult enough, there were also buildings which could block the banana’s trajectory.

This time you are close to the end of a game where, coincidentally, both gorillas were located at the same height (equal to 0). So, to be more precise, your gorilla is a point located at coordinates (0,0) and the opponent’s gorilla is located at the coordinates (d,0). Between the two gorillas there are N buildings (vertical line segments), having different heights. You want to finish the game as soon as possible so you want this shot to be the last one. Therefore, the banana (which is also a point) should be thrown in such a way that it should hit the opponent’s gorilla, but not the buildings (although it may touch the top of any building). Furthermore, in order to prove your superior skills to your opponent, you want to choose the minimum speed v for throwing the banana (but you may choose any angle u between 0 and π/2).
When solving this problem, you should make use of the value of the gravitational acceleration g (given as part of the input) and the following laws of motion:
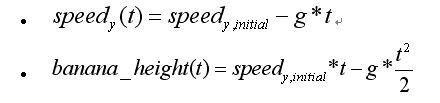

This time you are close to the end of a game where, coincidentally, both gorillas were located at the same height (equal to 0). So, to be more precise, your gorilla is a point located at coordinates (0,0) and the opponent’s gorilla is located at the coordinates (d,0). Between the two gorillas there are N buildings (vertical line segments), having different heights. You want to finish the game as soon as possible so you want this shot to be the last one. Therefore, the banana (which is also a point) should be thrown in such a way that it should hit the opponent’s gorilla, but not the buildings (although it may touch the top of any building). Furthermore, in order to prove your superior skills to your opponent, you want to choose the minimum speed v for throwing the banana (but you may choose any angle u between 0 and π/2).
When solving this problem, you should make use of the value of the gravitational acceleration g (given as part of the input) and the following laws of motion:
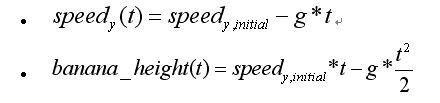
输入解释
The first line of input contains an integer number T, representing the number of test cases to follow. The first line of each test case contains 3 numbers, separated by blanks: an integer d (1<=d<=1.000.000), a floatin point number g (1<=g<=10) and an integer N (0<=N<=50.000). The ith of the next N lines contains two integer numbers, separated by one blank: Xi (1<= Xi<d) and Hi (1<=Hi<=1.000.000). Xi is the X coordinate of the ith building and Hi is its height. Furthermore, Xi<Xi+1.
输出解释
For each of the T test cases print one line containing the minimum value of the speed required to throw the banana. Print this value with 3 decimal digits, rounded (up or down) according to the 4th decimal digit.
输入样例
2 1 9.8 0 1000 1 1 500 10000
输出样例
3.130 141.466
来自杭电HDUOJ的附加信息
| Author | Mugurel Ionut Andreica |
| Recommend | lcy |
最后修改于 2020-10-25T22:48:12+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 2000/2000MS(Java/Others) | 65535/65535K(Java/Others) |
登陆或注册以提交代码