当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
3960:Binary Operation
题目描述
Consider a binary operation __poj_jax_start__\odot__poj_jax_end__ defined on digits 0 to 9. __poj_jax_start__\odot__poj_jax_end__: {0, 1, ..., 9} × {0, 1, ..., 9} __poj_jax_start__\to__poj_jax_end__ {0, 1, ..., 9}, such that 0 __poj_jax_start__\odot__poj_jax_end__ 0 = 0.
A binary operation __poj_jax_start__\otimes__poj_jax_end__ is a generalization of __poj_jax_start__\odot__poj_jax_end__ to the set of non-negative integers, __poj_jax_start__\otimes__poj_jax_end__: __poj_jax_start__\mathbb{Z}__poj_jax_end__0+ × __poj_jax_start__\mathbb{Z}__poj_jax_end__0+ __poj_jax_start__\to__poj_jax_end__ __poj_jax_start__\mathbb{Z}__poj_jax_end__0+. The result of a __poj_jax_start__\otimes__poj_jax_end__ b is defined in the following way: if one of the numbers a and b has fewer digits than the other in decimal notation, then append leading zeroes to it, so that the numbers are of the same length;
then apply the operation __poj_jax_start__\odot__poj_jax_end__ digit-wise to the corresponding digits of a and b.
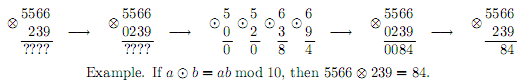
Let us define __poj_jax_start__\otimes__poj_jax_end__ to be left-associative, that is, a __poj_jax_start__\otimes__poj_jax_end__ b __poj_jax_start__\otimes__poj_jax_end__ c is to be interpreted as (a __poj_jax_start__\otimes__poj_jax_end__ b) __poj_jax_start__\otimes__poj_jax_end__ c.
Given a binary operation __poj_jax_start__\odot__poj_jax_end__ and two non-negative integers a and b, calculate the value of a __poj_jax_start__\otimes__poj_jax_end__ (a + 1) __poj_jax_start__\otimes__poj_jax_end__ (a + 2) __poj_jax_start__\otimes__poj_jax_end__ ... __poj_jax_start__\otimes__poj_jax_end__ (b - 1) __poj_jax_start__\otimes__poj_jax_end__ b.
A binary operation __poj_jax_start__\otimes__poj_jax_end__ is a generalization of __poj_jax_start__\odot__poj_jax_end__ to the set of non-negative integers, __poj_jax_start__\otimes__poj_jax_end__: __poj_jax_start__\mathbb{Z}__poj_jax_end__0+ × __poj_jax_start__\mathbb{Z}__poj_jax_end__0+ __poj_jax_start__\to__poj_jax_end__ __poj_jax_start__\mathbb{Z}__poj_jax_end__0+. The result of a __poj_jax_start__\otimes__poj_jax_end__ b is defined in the following way: if one of the numbers a and b has fewer digits than the other in decimal notation, then append leading zeroes to it, so that the numbers are of the same length;
then apply the operation __poj_jax_start__\odot__poj_jax_end__ digit-wise to the corresponding digits of a and b.
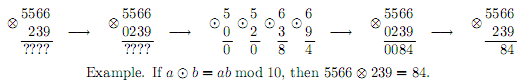
Let us define __poj_jax_start__\otimes__poj_jax_end__ to be left-associative, that is, a __poj_jax_start__\otimes__poj_jax_end__ b __poj_jax_start__\otimes__poj_jax_end__ c is to be interpreted as (a __poj_jax_start__\otimes__poj_jax_end__ b) __poj_jax_start__\otimes__poj_jax_end__ c.
Given a binary operation __poj_jax_start__\odot__poj_jax_end__ and two non-negative integers a and b, calculate the value of a __poj_jax_start__\otimes__poj_jax_end__ (a + 1) __poj_jax_start__\otimes__poj_jax_end__ (a + 2) __poj_jax_start__\otimes__poj_jax_end__ ... __poj_jax_start__\otimes__poj_jax_end__ (b - 1) __poj_jax_start__\otimes__poj_jax_end__ b.
输入解释
The first ten lines of the input file contain the description of the binary operation __poj_jax_start__\odot__poj_jax_end__. The i-th line of the input file contains a space-separated list of ten digits - the j-th digit in this list is equal to (i - 1) __poj_jax_start__\odot__poj_jax_end__ (j - 1).
The first digit in the first line is always 0.
The eleventh line of the input file contains two non-negative integers a and b (0 <= a <= b <= 1018).
The first digit in the first line is always 0.
The eleventh line of the input file contains two non-negative integers a and b (0 <= a <= b <= 1018).
输出解释
Output a single number – the value of a __poj_jax_start__\otimes__poj_jax_end__ (a + 1) __poj_jax_start__\otimes__poj_jax_end__ (a + 2) __poj_jax_start__\otimes__poj_jax_end__ ... __poj_jax_start__\otimes__poj_jax_end__ (b - 1) __poj_jax_start__\otimes__poj_jax_end__ b without extra leading zeroes.
输入样例
0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 0 2 3 4 5 6 7 8 9 0 1 3 4 5 6 7 8 9 0 1 2 4 5 6 7 8 9 0 1 2 3 5 6 7 8 9 0 1 2 3 4 6 7 8 9 0 1 2 3 4 5 7 8 9 0 1 2 3 4 5 6 8 9 0 1 2 3 4 5 6 7 9 0 1 2 3 4 5 6 7 8 0 10
输出样例
15
最后修改于 2020-10-29T07:16:39+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 3000 | 65536 |
登陆或注册以提交代码