当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
3925:Minimal Ratio Tree
题目描述
For a tree, which nodes and edges are all weighted, the ratio of it is calculated according to the following equation.
__poj_jax_start__Ratio=\frac{\sum{edgeweight}}{\sum{nodeweight}}__poj_jax_end__
Given a complete graph of n nodes with all nodes and edges weighted, your task is to find a tree, which is a sub-graph of the original graph, with m nodes and whose ratio is the smallest among all the trees of m nodes in the graph.
Given a complete graph of n nodes with all nodes and edges weighted, your task is to find a tree, which is a sub-graph of the original graph, with m nodes and whose ratio is the smallest among all the trees of m nodes in the graph.
输入解释
Input contains multiple test cases. The first line of each test case contains two integers n (2<=n<=15) and m (2<=m<=n), which stands for the number of nodes in the graph and the number of nodes in the minimal ratio tree. Two zeros end the input. The next line contains n numbers which stand for the weight of each node. The following n lines contain a diagonally symmetrical n×n connectivity matrix with each element shows the weight of the edge connecting one node with another. Of course, the diagonal will be all 0, since there is no edge connecting a node with itself.
All the weights of both nodes and edges (except for the ones on the diagonal of the matrix) are integers and in the range of [1, 100].
The figure below illustrates the first test case in sample input. Node 1 and Node 3 form the minimal ratio tree.
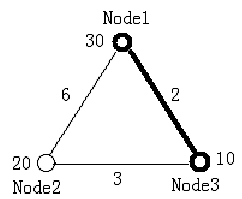
All the weights of both nodes and edges (except for the ones on the diagonal of the matrix) are integers and in the range of [1, 100].
The figure below illustrates the first test case in sample input. Node 1 and Node 3 form the minimal ratio tree.

输出解释
For each test case output one line contains a sequence of the m nodes which constructs the minimal ratio tree. Nodes should be arranged in ascending order. If there are several such sequences, pick the one which has the smallest node number; if there's a tie, look at the second smallest node number, etc. Please note that the nodes are numbered from 1.
输入样例
3 2 30 20 10 0 6 2 6 0 3 2 3 0 2 2 1 1 0 2 2 0 0 0
输出样例
1 3 1 2
最后修改于 2020-10-29T07:15:40+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 1000 | 65536 |
登陆或注册以提交代码