当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
3808:Malfatti Circles
Special Judge 特殊评判题目描述
The configuration of three circles packed inside a triangle such that each circle is tangent to the other two circles and to two of the edges of the triangle has been studied by many mathematicians for more than two centuries. Existence and uniqueness of such circles for an arbitrary triangle are easy to prove. Many methods of numerical calculation or geometric construction of such circles from an arbitrarily given triangle have been discovered. Today, such circles are called the Malfatti circles.
Figure 7 illustrates an example. The Malfatti circles of the triangle with the vertices (20, 80), (-40, -20) and (120, -20) are approximately
the circle with the center (24.281677, 45.219486) and the radius 21.565935,
the circle with the center (3.110950, 4.409005) and the radius 24.409005, and
the circle with the center (54.556724, 7.107493) and the radius 27.107493.
Figure 8 illustrates another example. The Malfatti circles of the triangle with the vertices (20, -20), (120, -20) and (-40, 80) are approximately
the circle with the center (25.629089, -10.057956) and the radius 9.942044,
the circle with the center (53.225883, -0.849435) and the radius 19.150565, and
the circle with the center (19.701191, 19.203466) and the radius 19.913790.
Your mission is to write a program to calculate the radii of the Malfatti circles of the given triangles.
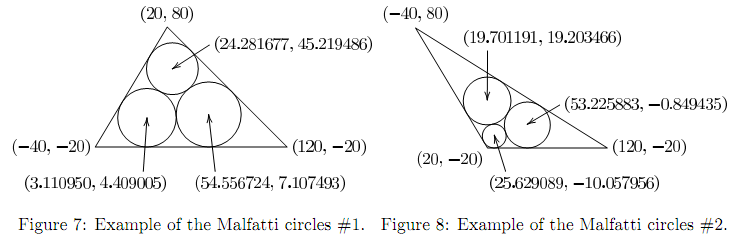
Figure 7 illustrates an example. The Malfatti circles of the triangle with the vertices (20, 80), (-40, -20) and (120, -20) are approximately
the circle with the center (24.281677, 45.219486) and the radius 21.565935,
the circle with the center (3.110950, 4.409005) and the radius 24.409005, and
the circle with the center (54.556724, 7.107493) and the radius 27.107493.
Figure 8 illustrates another example. The Malfatti circles of the triangle with the vertices (20, -20), (120, -20) and (-40, 80) are approximately
the circle with the center (25.629089, -10.057956) and the radius 9.942044,
the circle with the center (53.225883, -0.849435) and the radius 19.150565, and
the circle with the center (19.701191, 19.203466) and the radius 19.913790.
Your mission is to write a program to calculate the radii of the Malfatti circles of the given triangles.

输入解释
The input is a sequence of datasets. A dataset is a line containing six integers x1, y1, x2, y2, x3 and y3 in this order, separated by a space. The coordinates of the vertices of the given triangle are (x1, y1), (x2, y2) and (x3, y3), respectively. You can assume that the vertices form a triangle counterclockwise. You can also assume that the following two conditions hold.
All of the coordinate values are greater than -1000 and less than 1000.
None of the Malfatti circles of the triangle has a radius less than 0.1.
The end of the input is indicated by a line containing six zeros separated by a space.
All of the coordinate values are greater than -1000 and less than 1000.
None of the Malfatti circles of the triangle has a radius less than 0.1.
The end of the input is indicated by a line containing six zeros separated by a space.
输出解释
For each input dataset, three decimal fractions r1, r2 and r3 should be printed in a line in this order separated by a space. The radii of the Malfatti circles nearest to the vertices with the coordinates (x1, y1), (x2, y2) and (x3, y3) should be r1, r2 and r3, respectively.
None of the output values may have an error greater than 0.0001. No extra character should appear in the output.
None of the output values may have an error greater than 0.0001. No extra character should appear in the output.
输入样例
20 80 -40 -20 120 -20 20 -20 120 -20 -40 80 0 0 1 0 0 1 0 0 999 1 -999 1 897 -916 847 -972 890 -925 999 999 -999 -998 -998 -999 -999 -999 999 -999 0 731 -999 -999 999 -464 -464 999 979 -436 -955 -337 157 -439 0 0 0 0 0 0
输出样例
21.565935 24.409005 27.107493 9.942044 19.150565 19.913790 0.148847 0.207107 0.207107 0.125125 0.499750 0.499750 0.373458 0.383897 0.100456 0.706768 0.353509 0.353509 365.638023 365.638023 365.601038 378.524085 378.605339 378.605339 21.895803 22.052921 5.895714
最后修改于 2020-10-29T07:12:05+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 1000 | 65536 |
登陆或注册以提交代码