当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
3792:Area of Polycubes
题目描述
A polycube is a solid made by gluing together unit cubes (one unit on each edge) on one or more faces. The figure in the lower-left is not a polycube because some cubes are attached along an edge.
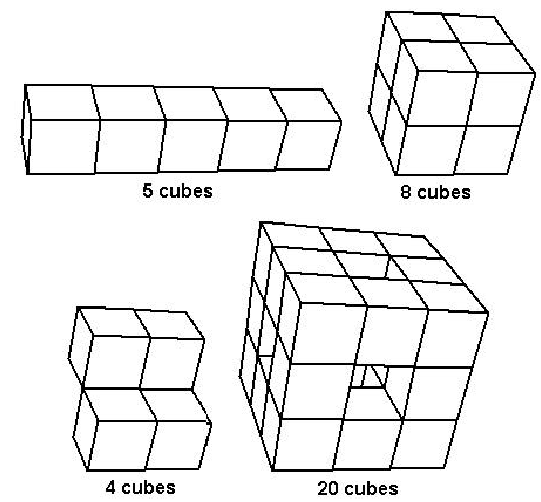
For this problem, the polycube will be formed from unit cubes centered at integer lattice points in 3-space. The polycube will be built up one cube at a time, starting with a cube centered at (0,0,0). At each step of the process (after the first cube), the next cube must have a face in common with a cube previously included and not be the same as a block previously included. For example, a 1-by-1-by-5 block (as shown above in the upper-left polycube) could be built up as:
(0,0,0) (0,0,1) (0,0,2) (0,0,3) (0,0,4)
and a 2-by-2-by-2 cube (upper-right figure) could be built as:
(0,0,0) (0,0,1) (0,1,1) (0,1,0) (1,0,0) (1,0,1) (1,1,1) (1,1,0)
Since the surface of the polycube is made up of unit squares, its area is an integer.
Write a program which takes as input a sequence of integer lattice points in 3-space and determines whether is correctly forms a polycube and, if so, what the surface area of the polycube is.

For this problem, the polycube will be formed from unit cubes centered at integer lattice points in 3-space. The polycube will be built up one cube at a time, starting with a cube centered at (0,0,0). At each step of the process (after the first cube), the next cube must have a face in common with a cube previously included and not be the same as a block previously included. For example, a 1-by-1-by-5 block (as shown above in the upper-left polycube) could be built up as:
(0,0,0) (0,0,1) (0,0,2) (0,0,3) (0,0,4)
and a 2-by-2-by-2 cube (upper-right figure) could be built as:
(0,0,0) (0,0,1) (0,1,1) (0,1,0) (1,0,0) (1,0,1) (1,1,1) (1,1,0)
Since the surface of the polycube is made up of unit squares, its area is an integer.
Write a program which takes as input a sequence of integer lattice points in 3-space and determines whether is correctly forms a polycube and, if so, what the surface area of the polycube is.
输入解释
The first line of input contains a single integer N, (1 <= N <= 1000) which is the number of data sets that follow. Each data set consists of multiple lines of input. The first line contains the number of points P, (1 <= P <= 100) in the problem instance. Each succeeding line contains the centers of the cubes, eight to a line (except possibly for the last line). Each center is given as 3 integers, separated by commas. The points are separated by a single space.
输出解释
For each data set, you should generate one line of output with the following values: The data set number as a decimal integer (start counting at one), a space and the surface area of the polycube if it is correctly formed, OR, if it is not correctly formed, the string “NO” a space and the index (starting with 1) of the first cube which does not share a face with a previous cube. Note that the surface area includes the area of any included holes.
输入样例
4 5 0,0,0 0,0,1 0,0,2 0,0,3 0,0,4 8 0,0,0 0,0,1 0,1,0 0,1,1 1,0,0 1,0,1 1,1,0 1,1,1 4 0,0,0 0,0,1 1,1,0 1,1,1 20 0,0,0 0,0,1 0,0,2 0,1,2 0,2,2 0,2,1 0,2,0 0,1,0 1,0,0 2,0,0 1,0,2 2,0,2 1,2,2 2,2,2 1,2,0 2,2,0 2,1,0 2,1,2 2,0,1 2,2,1
输出样例
1 22 2 24 3 NO 3 4 72
最后修改于 2020-10-29T07:11:32+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 1000 | 65536 |
登陆或注册以提交代码