3788：Interior Points of Lattice Polygons

A lattice point is a point with integer coordinates. A lattice polygon is a polygon with all vertices lattice points.



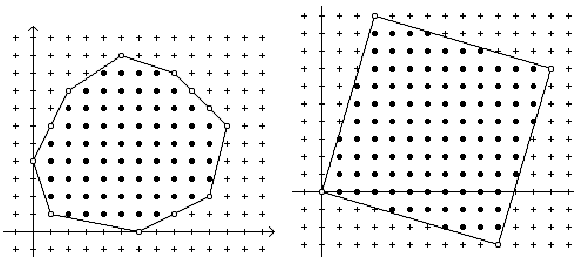
The lattice points on the boundary of the polygon are boundary points (open dots in the figure above) and the points inside and not on the polygon are interior points (filled in dots in the figure above).

A polygon is convex if any line segment between two points of the polygon is inside (or on the boundary of) the polygon. Equivalently, the interior angle at each polygon vertex is less than 180 degrees. Note that any line between two points inside (and not on the boundary of) the polygon is entirely inside (and not on the boundary of) the polygon.

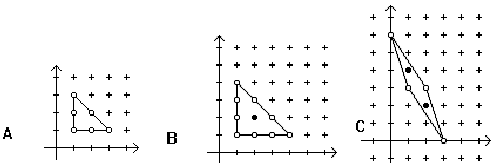
The interior points of a convex lattice polygon on any horizontal line form a single segment from a leftmost point to a rightmost point (which may be the same). Note that there may be no interior points (A), or only one (B), or isolated points (C) as shown in the figures below.



Write a program that reads the vertices of a convex lattice polygon in standard order and outputs the interior points as a list of horizontal line segments. The vertices of a lattice polygon are in standard order if:
a) The first vertex is the one with the largest y value. If two vertices have the same y value, the one with the smaller x value is the first.
b) Vertices are given in clockwise order around the polygon.

The first line of input contains a single integer P, (1 ≤ P ≤ 1000), which is the number of data sets that follow. The first line of each data set contains the data set number, followed by a space, followed by a decimal integer giving the number vertices N, (3 ≤ N ≤ 50), of the polygon. The remaining lines in the data set contain the vertices, one per line in standard order. Each line contains the decimal integer x coordinate, a space and the decimal integer y coordinate.

For each data set there are multiple lines of output. The first line contains a decimal integer giving the data set number followed by a single space, followed by a decimal integer giving the number of horizontal lines which contain interior points (this may be zero (0) or more). The lines of interior points, if any, follow, one per line in order of decreasing y value. Each line contains the decimal integer y coordinate, a single space and the decimal integer x coordinate of the left most point, a single space and the decimal integer x coordinate of the right most point.