3576：Language Recognition

Deterministic Final-State Automaton (DFA) is a directed multigraph whose vertices are called states and edges are called transitions. Each DFA transition is labeled with a single letter. Moreover, for each state s and each letter l there is at most one transition that leaves s and is labeled with l. DFA has a single starting state and a subset of final states. DFA defines a language of all words that can be constructed by writing down the letters on a path from the starting state to some final state.

Given a language with a finite set of words it is always possible to construct a DFA that defines this language. The picture on the left shows such DFA for the language consisting of three words: fix, foo, ox. However, this DFA has 7 states, which is not optimal. The DFA on the right defines the same language with just 5 states.

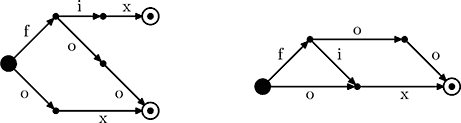
Your task is to find the minimum number of states in a DFA that defines the given language.

The first line of the input file contains a single integer number n (1 ≤ n ≤ 5 000) — the number of words in the language. It is followed by n lines with a word on each line. Each word consists of 1 to 30 lowercase Latin letters from “a” to “z”. All words in the input file are different.

Write to the output file a single integer number — the minimal number of states in a DFA that defines the language from the input file.