当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
3562:“Roman” corridor
题目描述
Let’s remind the notation of Roman numerals. The notation is for natural numbers from 1 to 3999. Capital Latin letters ‘I’, ‘V’, ‘X’, ‘L’, ‘C’, ‘D’, ‘M’ and their combinations are used to represent so called atomic numbers (see the table below).
| 1 – I | 40 – XL | 500 – D |
| 4 – IV | 50 – L | 900 – CM |
| 5 – V | 90 – XC | 1000 – M |
| 9 – IX | 100 – C | |
| 10 – X | 400 – CD |
To put down a number N it is necessary to find the greatest atomic number K which is not greater then N. The Roman notation of the found number K is put down, and the process is repeated for (N-K).
The Roman numerals are put down from left to right without spaces. Thus, the number 999 in the Roman notation is CMXCIX (but not IM, as somebody may think). You need to pass through a rectangular corridor. The corridor is n meters width and m meters long (1 ≤ n, m ≤ 15, n*m ≤ 100). It is laid out by square tiles. Each tile is 1 meter width and has a ‘Roman’ symbol on it: ‘I’, ‘V’, ‘X’, ‘L’, ‘C’, ‘D’ or ‘M’. When passing the corridor, you move from one tile to another. From the current tile you may only move to one of adjacent tiles, vertically or horizontally (but not across). You start at the left and end at the right (see the picture below).
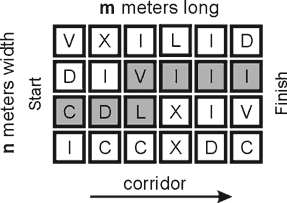
Can you pass through the corridor so that the sequence of symbols on the tiles composing your path was a correct number in the Roman notation? Among all possible solutions you need to find the minimal number.
输入解释
The first line contains numbers n and m, separated by one or more spaces. Each of the next n lines consists of m characters describing tiles.
输出解释
The output contains one line with the found Roman number or the word NO if it is impossible to pass through the corridor in the required way.
输入样例
4 6 VXILID DIVIII CDLXIV ICCXDC
输出样例
CDLVIII
最后修改于 2020-10-29T07:04:37+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 1000 | 65536 |