3555：Cocktail

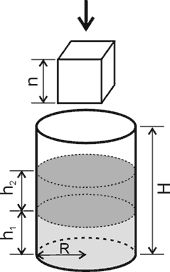
Cylindrical vessel of height H (0 < H ≤ 10 000) and bottom radius R (0 < R ≤ 10000) stands on a horizontal surface. There are two liquids in the vessel. The liquids have different density and do not mix. D₁ and D₂ are densities of the first and the second liquids respectively, 0 < D₂ < D₁ ≤ 10000. h₁ and h₂ are heights of layers of the first and the second liquids, h₁, h₂ > 0, h₁ + h₂ ≤ H. There is a cube made of a solid material. The cube’s edge length is n (0 < n ≤ 1.4*R), the material’s density is D (0 < D ≤ 10 000). The cube is put down into the vessel in such a way that one of its sides is horizontal.  Pay attention that some amount of liquid may pour out of the vessel. As a result of the operation the cube floats in liquids or lie on the vessel bottom.

You need to calculate the height of the vessel which is occupied by the liquids after the cube is put down into the vessel. You may neglect damping and some other physical effects, but you should take into account Archimedean Principle.

The only line of the input contains numbers H, R, D₁, h₁, D₂, h₂, D and n separated by spaces. All the numbers are real. Each of them does not contain more than three digits in its fractional part.

The output contains one real number – the height you need to calculate. Absolute error must not exceed 10⁻³.