3426：Doors and... more doors

When wondering through the labyrinth, the goal is usually to find some kind of door. Well, not this time.

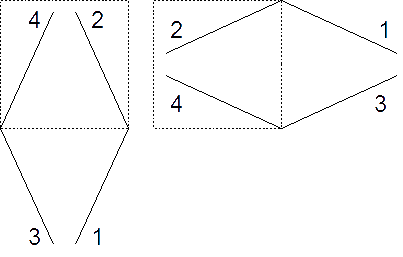
A labyrinth consists of N × N cells, each 1 × 1 meter in size. Cells are separated by doors. Each door opens in a specific direction (as shown on the picture):

1. left outwards;
2. left inwards;
3. right outwards;
4. right inwards.

So a cell can be represented by two numbers describing doors on its eastern and southern sides according to the list above. The doors are just slightly less then 1 meter in width. The traveler in the labyrinth is also slightly less then 1 meter in diameter, so he has following limitations:

* He can not pull doors, only push them.
* After opening the door and entering the cell it leads to, he can not take a turn in the direction where the door opened, because the passage is blocked by the door. Doors have springs and close automatically when traveler leaves the cell.

Your program must find the shortest path for the traveler from north-western cell (1, 1) to south-eastern cell (N, N).

Input file contains labyrinth size N followed by 2 × N² numbers describing doors for each cell row by row. As there are no doors leading outside of labyrinth, values for eastern doors in the last column and southern doors in the last row are zero.

Constraints

1 ≤ N ≤ 1000

Output file must contain the shortest path as a list of cell coordinates (column number, then row number), including both (1, 1) and (N, N) cells. If there are several solutions with the same length, output any one of them. If it is impossible to get to a destination cell, output a singe zero.