3310：Caterpillar

题目描述

An undirected graph is called a caterpillar if it is connected, has no cycles, and there is a path in the graph where every node is either on this path or a neighbor of a node on the path. This path is called the spine of the caterpillar and the spine may not be unique. You are simply going to check graphs to see if they are caterpillars.

For example, the left graph below is not a caterpillar, but the right graph is. One possible spine is
shown by dots.

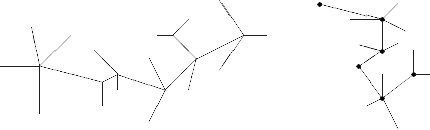
输入解释

There will be multiple test cases. Each test case starts with a line containing n indicating the number of nodes, numbered 1 through n (a value of n = 0 indicates end-of-input). The next line will contain an integer e indicating the number of edges. Starting on the following line will be e pairs n₁ n₂ indicating an undirected edge between nodes n₁ and n₁. This information may span multiple lines. You may assume that n ≤ 100 and e ≤ 300. Do not assume that the graphs in the test cases are connected or acyclic.

输出解释

For each test case generate one line of output. This line should either be

Graph g is a caterpillar.
or
Graph g is not a caterpillar.

as appropriate, where g is the number of the graph, starting at 1.

输入样例

22
21
1 2 2 3 2 4 2 5 2 6 6 7 6 10 10 8 9 10 10 12 11 12 12 13 12 17
18 17 15 17 15 14 16 15 17 20 20 21 20 22 20 19
16
15
1 2 2 3 5 2 4 2 2 6 6 7 6 8 6 9 9 10 10 12 10 11 10 14 10 13 13 16 13 15
0

输出样例

Graph 1 is not a caterpillar.
Graph 2 is a caterpillar.

该题目是Virtual Judge题目，来自北京大学POJ

题目来源 East Central North America 2006

源链接： POJ-3310

最后修改于 2020-10-29T06:58:17+00:00 由爬虫自动更新

共提交 0 次

通过率 --%

时间上限	内存上限
2000	65536