当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
3221:Diamond Puzzle
题目描述
A diamond puzzle is played on a tessellated hexagon like the one shown in Figure 1 below. And in this problem the faces produced by the tessellation are identified as they are numbered in the same figure. If two faces share a side, they are called neighboring faces. Thus, even-numbered faces have three neighboring faces, while odd-numbered faces have only two. At any point during the play of the puzzle, six of the seven faces hold a unique digit ranging from 1 to 6, and the other one is empty. A move in the puzzle is to move a digit from one face to a neighboring empty one.
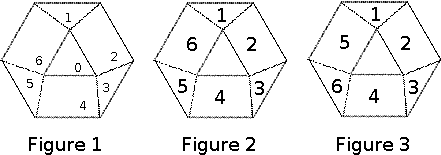
Starting from any configuration, some series of moves can always make the puzzle look identical to either one shown in Figures 2 and 3. Your task is to calculate the minimum number of moves to make it become the one in Figure 2.
输入解释
The input contains multiple test cases. The first contains an integer N (0 ≤ N ≤ 5,040), the number of test cases. Then follow N lines, each with a permutation of {0, 1, 2, 3, 4, 5, 6} describing a starting configuration of the puzzle. The ith digit in the permutation is the one in the face numbered i − 1. A zero means the face is empty.
输出解释
For each test cases, output the minimum number of moves the configuration takes to reach the one shown in Figure 2. If this is impossible, just output “-1” and nothing else.
输入样例
3 1324506 2410653 0123456
输出样例
10 -1 0
最后修改于 2020-10-29T06:56:09+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 2000 | 131072 |