当前你的浏览器版本过低，网站已在兼容模式下运行，兼容模式仅提供最小功能支持，网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。

建议使用的浏览器：

谷歌Chrome 火狐Firefox Opera浏览器 微软Edge浏览器 QQ浏览器 360浏览器 傲游浏览器

3215：Median of Lines

题目描述

In the Cartesian plane, there are n (odd) distinct lines fi(x) = ai + xbi (i = 1, 2, …, n). For each x, F(x) denotes the median of {f1(x), f2(x), ..., fn(x)}. You are required to find the solution space of the equation F(x) = 0.

输入解释

The input contains multiple test cases. Each test case have n + 1 lines the first one of which contains n (1 < n < 105 and odd). Then n lines follow, each of which contains two integers ai and bi (|ai| ≤ 108, 0 ≤ bi < 108). A zero follows the last test case.

输出解释
For each test case, output the solution space as an interval on a separate line. Interval boundaries should be rounded to two digits beyond the decimal point. “+inf” and “-inf” are used to represent positive and negative infinities. The solution space will form at most one interval in this problem. If the solution space is empty, just output “-1”.
输入样例 
3
0 0
1 0
0 1
3
0 0
1 2
1 1
3
1 0
2 0
3 0
3
1 1
1 2
1 3
3
0 0 
1 0
-1 0
0
输出样例 
(-inf,0.00]
[-1.00,-0.50]
-1
[-0.50,-0.50]
(-inf,+inf)
提示

Be cautious about outputting “-0.00”.

Illustration of the second test case in the sample input:

该题目是Virtual Judge题目，来自 北京大学POJ
题目来源 POJ Monthly--2007.04.01, dearboy
源链接： POJ-3215
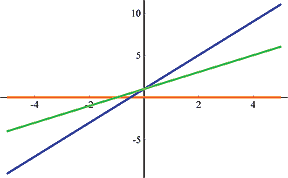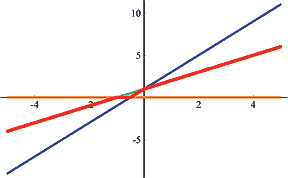最后修改于 2020-10-29T06:56:02+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
时间上限 内存上限
6000 131072