3197：Continuous Fractions

A simple continuous fraction has the form:

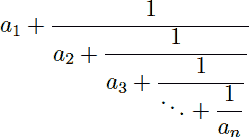
where the a_i’s are integer numbers.

The previous continuous fraction could be noted as [a₁, a₂, …, a_n]. It is not difficult to show that any rational number ^p⁄_q, with integers p > q > 0, can be represented in a unique way by a simple continuous fraction with n terms, such that ^p⁄_q = [a₁, a₂, …, a_n−1, 1], where n and the a_i’s are positive natural numbers.

Your task is to find and print the simple continuous fraction that corresponds to a given rational number.

Cases must be analyzed in the order that are read from the input. Output for each case will consist of several lines. The first line indicates the case number, starting at 1, using the format:

Case i:

replacing i by the corresponding case number. The second line displays the input data in the form p / q.

The remaining lines must contain the continuous fraction corresponding to the rational number, ^p⁄_q, specified in the given input line. The continuous fraction must be printed accordingly to the following rules:

• Horizontal bars are formed by sequences of dashes ‘-’.
• The width of each horizontal bar is exactly equal to the width of the denominator under it.
• Blank characters should be printed using periods ‘.’.
• The number on a fraction numerator must be printed center justified. That is, the number of spaces at either side must be same, if possible; in other case, one more space must be added at the right side.