3194：Equidivisions

An equidivision of an n × n square array of cells is a partition of the n² cells in the array in exactly n sets, each one with n contiguous cells. Two cells are contiguous when they have a common side.

A good equidivision is composed of contiguous regions. The figures show a good and a wrong equidivision for a 5 × 5 square:

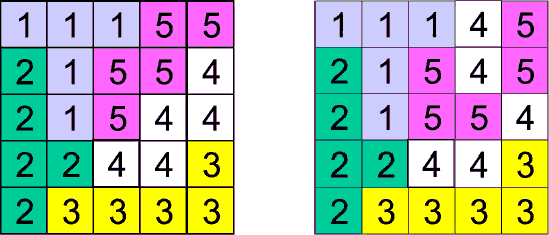
Note that in the second example the cells labeled with 4 describe three non-contiguous regions and cells labeled with 5 describe two non-contiguous regions. You must write a program that evaluates if an equidivision of the cells in a square array is good or not.

It is understood that a cell in an n × n square array is denoted by a pair (i, j), with 1 ≤ i, j ≤ n. The input file contains several test cases. Each test case begins with a line indicating n, 0 < n < 100, the side of the square array to be partitioned. Next, there are n − 1 lines, each one corresponding to one partition of the cells of the square, with some non-negative integer numbers. Consecutive integers in a line are separated with a single blank character. A line of the form

a₁a₂a₃a₄…

means that cells denoted with the pairs (a₁, a₂), (a₃, a₄), … belong to one of the areas in the partition. The last area in the partition is defined by those cells not mentioned in the n − 1 given lines. If a case begins with n = 0 it means that there are no more cases to analyze.