当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
3150:Cellular Automaton
题目描述
A cellular automaton is a collection of cells on a grid of specified shape that evolves through a number of discrete time steps according to a set of rules that describe the new state of a cell based on the states of neighboring cells. The order of the cellular automaton is the number of cells it contains. Cells of the automaton of order n are numbered from 1 to n.
The order of the cell is the number of different values it may contain. Usually, values of a cell of order m are considered to be integer numbers from 0 to m − 1.
One of the most fundamental properties of a cellular automaton is the type of grid on which it is computed. In this problem we examine the special kind of cellular automaton — circular cellular automaton of order n with cells of order m. We will denote such kind of cellular automaton as n,m-automaton.
A distance between cells i and j in n,m-automaton is defined as min(|i − j|, n − |i − j|). A d-environment of a cell is the set of cells at a distance not greater than d.
On each d-step values of all cells are simultaneously replaced by new values. The new value of cell i after d-step is computed as a sum of values of cells belonging to the d-enviroment of the cell i modulo m.
The following picture shows 1-step of the 5,3-automaton.
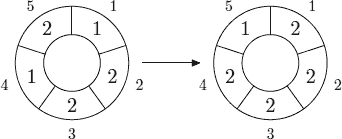
The problem is to calculate the state of the n,m-automaton after k d-steps.
输入解释
The first line of the input file contains four integer numbers n, m, d, and k (1 ≤ n ≤ 500, 1 ≤ m ≤ 1 000 000, 0 ≤ d < n⁄2 , 1 ≤ k ≤ 10 000 000). The second line contains n integer numbers from 0 to m − 1 — initial values of the automaton’s cells.
输出解释
Output the values of the n,m-automaton’s cells after k d-steps.
输入样例
sample input #1 5 3 1 1 1 2 2 1 2 sample input #2 5 3 1 10 1 2 2 1 2
输出样例
sample output #1 2 2 2 2 1 sample output #2 2 0 0 2 2
来自北京大学POJ的附加信息
| Case time limit(单组数据时间限制) | 2000MS |
最后修改于 2020-10-29T06:54:19+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 12000 | 65536 |