3124：The Bookcase

No wonder the old bookcase caved under the massive piles of books Tom had stacked
on it. He had better build a new one, this time large enough to hold all of his books. Tomfinds it practical to have the books close at hand when he works at his desk. Therefore, he is imagining a compact solution with the bookcase standing on the back of the desk. Obviously, this would put some restrictions on the size of the bookcase, it should preferably be as small as possible. In addition, Tom would like the bookcase to have exactly three shelves for aesthetical reasons.

Wondering how small his bookcase could be, he models the problem as follows. He measures the height hi and thickness ti of each book i and he seeks a partition of the books in three non-empty sets S1, S2, S3 such that 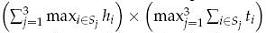is minimized, i.e. the area of the bookcase as seen when standing in front of it (the depth needed is obviously the largest width of all his books, regardless of the partition). Note that this formula does not give the exact area of the bookcase, since the actual shelves cause a small additional height, and the sides cause a small additional width. For simplicity, we will ignore this small discrepancy.

Thinking a moment on the problem, Tom realizes he will need a computer program to do the job.

The input begins with a positive number on a line of its own telling the number of test cases (at most 20). For each test case there is one line containing a single positive integer N, 3 ≤ N ≤ 70 giving the number of books. Then N lines follow each containing two positive integers hi, ti, satisfying 150 ≤ hi ≤ 300 and 5 ≤ ti ≤ 30, the height and thickness of book i respectively, in millimeters.

For each test case, output one line containing the minimum area (height times width) of a three-shelf bookcase capable of holding all the books, expressed in square millimeters.