3054：High Spies

You have been approached by a spy agency to determine the amount of contraband goods that are being traded among several nefarious countries. After being shipped from its country of origin, each container of goods is routed through at least one neutral port. At the port, the container are stored in a warehouse before being sent on their way, so you cannot trace individual containers from their country of origin to their final destination. Satellite cameras can tell you the number of containers travelling in each direction on each leg of the journey. They cannot distinguish individual containers, nor do you have information on the times individual containers have been observed. You know, however, that every container takes the shortest possible route to its destination.

The task is to determine both the maximum and minimum number of containers that could have been travelling from one country to another. The transport network that is observed is an unrooted tree, with countries as leaves and ports as internal nodes. For each edge the number of containers is given in two directions. You know from the description above that no container leaves a port in the direction it came from.

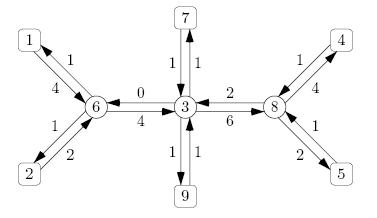
In the figure above we see six countries 1,2,4,5,7,9 and three ports 3,6,8. Although all edges on the route from country 1 to country 4 have a capacity of at least 4, it is not possible to send four container along this route. In that case, in port 6 one of the containers arriving from country 2 would be forced to return, which is forbidden.

This problem was taken from Dennis E. Shasha's monthly column Puzzling Adventures, published in Scientific American, July 2003.

The first line of the input contains a single number: the number of test cases to follow. Each test case describes a single unrooted tree, in the following format:

• One line with one integer n (3 <= n <= 10000): the number of nodes (countries and ports).
• n - 1 lines with four integers a, b, c1, c2 each(1 <= a, b <= n and 0 <= c1, c2 <= 1000), describing an edge from node a to (another) node b with c1 containers counted in the direction from a to b and c2 in the other direction.
• One line with two integers fr and to (1 <= fr, to <=n, fr != to): the begin and end nodes (countries, i.e., leaves in the tree).

Integers on the same line are separated by single spaces. The input satisfies Kirchhoff's law: in each port the number of incoming containers equals the number of outgoing containers. This in itself is not sufficient to guarantee the existence of a transport of containers that matches the description (as containers never move back from where they came). In each test case given a matching transport exists.

For every test case in the input, the output should contain a single line with two integers, separated by a single space, the minimum and maximum number of containers transported from fr to to fitting the data given.