当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
2961:Sylvester construction
题目描述
A Hadamard matrix of order n is an n x n matrix containing only 1s and -1s, called Hn, such that HnHnT = nIn where In is the n x n identity matrix. An interesting property of Hadamard matrices is that they have the maximum possible determinant of any n x n matrix with elements in the range [-1, 1]. Hadamard matrices have applications in errorcorrecting codes and weighing design problems.
The Sylvester construction is a way to create a Hadamard matrix of size 2n given Hn. H2n can be constructed as:
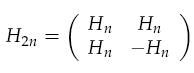
for example:
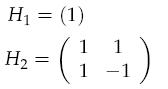
and so on.
In this problem you are required to print a part of a Hadamard matrix constructed in the way described above.
The Sylvester construction is a way to create a Hadamard matrix of size 2n given Hn. H2n can be constructed as:
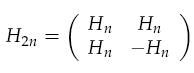
for example:
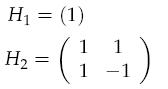
and so on.
In this problem you are required to print a part of a Hadamard matrix constructed in the way described above.
输入解释
The first number in the input is the number of test cases to follow. For each test case there are five integers: n, x, y, w and h. n will be between 1 and 262 (inclusive) and will be a power of 2. x and y specify the upper left corner of the sub matrix to be printed, w and h specify the width and height respectively. Coordinates are zero based, so 0 ≤ x,y < n. You can assume that the sub matrix will fit entirely inside the whole matrix and that 0 < w,h ≤ 20. There will be no more than 1000 test cases.
输出解释
For each test case print the sub matrix followed by an empty line.
输入样例
3 2 0 0 2 2 4 1 1 3 3 268435456 12345 67890 11 12
输出样例
1 1 1 -1 -1 1 -1 1 -1 -1 -1 -1 1 1 -1 -1 1 1 -1 -1 1 1 -1 -1 -1 -1 1 1 -1 -1 1 1 -1 -1 1 1 1 1 -1 -1 -1 -1 1 1 1 1 -1 1 -1 -1 1 -1 1 1 -1 1 -1 1 -1 -1 -1 -1 1 1 1 1 -1 -1 -1 -1 1 -1 1 1 -1 1 -1 -1 1 -1 -1 -1 -1 -1 -1 -1 1 1 1 1 1 -1 1 -1 1 -1 1 1 -1 1 -1 -1 1 1 -1 -1 1 1 1 1 -1 -1 1 1 -1 -1 1 1 -1 1 -1 -1 1 -1 -1 -1 1 1 1 1 1 1 1 1 1 -1 1 1 -1 1 -1 1 -1 1 -1
最后修改于 2020-10-29T06:48:36+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 1000 | 65536 |
登陆或注册以提交代码