2863：Mission Impossible

You have been hired to explore enemy territory. It is risky business, you know that. So, you'd better be prepared! The enemy has placed a number of security points all over his country, from which radars are detecting any moving vehicle within their range of cover. Any such detected object will be immediately destroyed. Fortunately enough, you have been given by your government a map of the enemy territory, consisting of coordinates and radius of coverage of each radar. You have also a list of local informers (together with their locations) that you should contact in order to obtain valuable information. Your mission is to try to contact one of these informers, preferably the one with highest insider-coefficient. The insider-coefficient of each informer is simply the distance from the informer to the border of the country, where such a distance is defined as the minimum over all distances from the location of the informer to each point of the border. In intuitive sense, the informer with highest insider-coefficient is that who is located as inside the country as possible, and will presumably have more valuable information about the country.

Your first thought is then to design a computer program which will check if there is a path from your initial location, always the point (2000, 2000), to any of the informers' location, without crossing any region which is covered by radar. Whenever possible, the program should indicate which reachable informer is the one to be contacted, according to the insider-coefficient criteria described above.



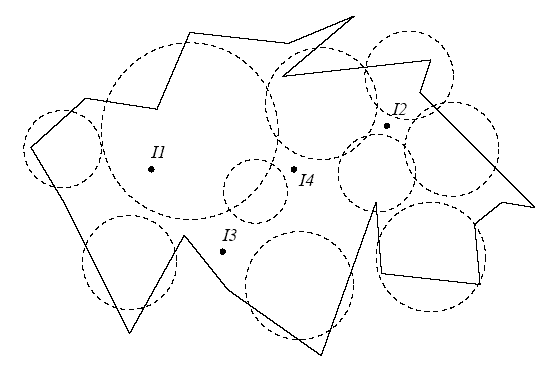
The enemy country has the shape of a simple polygon (not necessarily convex). Recall that a polygon is called simple if it is described by a single, non-intersecting boundary. The borders of the country will be given as a sequence of X,Y-coordinates corresponding to the sequence of vertexes of the polygon. You may assume that all the radar's centres and the informers' coordinates are located within the country's border. Notice, however, that the area covered by the radars might include regions outside the border.

In the sample scenario of Figure 1, informer I1 cannot be contacted since he is inside the region covered by radars. The informer I2, although outside the radar's region, can't be contacted either since any trip to his location would go through the deadly radar-covered regions. Both informers I3 and I4 could be contacted, so that informer I4 is chosen since his insider-coefficient is greater than that of I3.

The input consists of several test cases. The first line of each test case describes the border of the enemy country, in the format
B X1 Y1 X2 Y2 ... XB YB
where 3 <= B <= 1000 is the number of border points, and each Xi Yi is the coordinate of the i-th point in the border. The border of the country consists of line segments between points i and i + 1, and between points B and 1. The second line gives the number of informers and their respective positions, in the format
N X1 Y1 X2 Y2 ... XN YN
where 1 <= N <= 1000 is the number of informers, and Xi Yi is the coordinate of the i-th informer. The third line describes the position and radius of the radars, in the format
M X1 Y1 R1 X2 Y2 R2 ... XM YM RM
where 1 <= M <= 30 is the number of radars, Xi Yi is the coordinate of the i-th radar, and Ri is the radius of the i-th radar. All the coordinates are integers 0 <= X, Y <= 1000. The radius of the radars are integers in the range 1 <= R <= 1000. A test case where B = N = M = 0 indicates the end of the input. This test case must not be processed.

For each test case in the input, your program must produce one line containing either "Mission impossible" or "Contact informer K", where "K" is the index of the informer (as given in the input) with highest insider-coefficient which can be reached by the spy without going inside any radar coverage area. If there are more than one informer satisfying this condition, choose the one among them with lowest index.