2837：Silver Matrix

If a matrix satisfies the following conditions, we call it a silver matrix.

1. The dimensions of the matrix are n * n.
2. All its elements belong to the set S = {1, 2, 3, …, 2n - 1}.
3. For every integer i (1 <= i <= n), all elements in the i-th row and i-th column make the set {1, 2, 3, …, 2n - 1}.

For example, the following 4 * 4 matrix is a silver matrix:

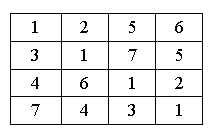
It is proved that silver matrix with size 2^K * 2^K always exists. And it is your job to find a silver matrix with size 2^K * 2^K.

The input contains only an integer K (1 <= K <= 9).

You may output any matrix with size 2^K * 2^K. To output a 2^K * 2^K matrix, you should output 2^K lines, and in each line output 2^K integers.