当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
2811:Packing Dominoes
Special Judge 特殊评判题目描述
A domino is a 2 x 1 oblong comprising two squares, each square marked with a set of "pips" denoting a non-negative integer. A blank square denotes the number 0 (zero).
In a standard " double-K " set of dominoes, each pair of integers in the range 0...K occurs on one domino. In other words, the dominoes are numbered:
(0, 0),(0, 1),...(0, K),(1, 1),...(1, K),(2, 2),...,(K, K)
Given a set of dominoes and a rectangular area of width w and height h , write a program to pack that entire set of dominoes into that area subject to the limitation that, whenever two dominoes touch one another either horizontally or vertically, the numbers on the touching squares must be identical. Note that the area might not be completely covered, and, space permitting, some dominoes might not touch any others.
In a standard " double-K " set of dominoes, each pair of integers in the range 0...K occurs on one domino. In other words, the dominoes are numbered:
(0, 0),(0, 1),...(0, K),(1, 1),...(1, K),(2, 2),...,(K, K)
Given a set of dominoes and a rectangular area of width w and height h , write a program to pack that entire set of dominoes into that area subject to the limitation that, whenever two dominoes touch one another either horizontally or vertically, the numbers on the touching squares must be identical. Note that the area might not be completely covered, and, space permitting, some dominoes might not touch any others.
输入解释
Input will consist of one or more lines, each containing 3 positive integers. The first integer, K , indicates the size of the set of dominoes - a "double-K set" as described above. The remaining integers, w and h , indicate the size of the area in which the dominoes should be placed, measured in units the same size as one of the constituent squares of a domino. The end of input will be signaled by a non-positive K value.
输出解释
For each line of input, print one line containing the values K(K<=3) , w , and h (w,h<=12), as defined above, followed either by a line with the string ``No packing is possible" or by a report consisting of (K+1)(K+2)/2 lines, each line describing one domino, ordered as described above in the definition of a ``doubleK " set.
Each line of that report will contain 6 integers
d1 d2 x1 y1 x2 y2
where d1 and d2 are the numbers on that domino, (x1, y1) is the coordinates of the number d1 in the packed layout, and (x2, y2) is the coordinates of number d2 . Coordinates are specified as integers with (0,0) denoting the lower-left corner of the packing area.
If multiple packings are possible, any packing meeting the criteria outlined above will be accepted.
Each line of that report will contain 6 integers
d1 d2 x1 y1 x2 y2
where d1 and d2 are the numbers on that domino, (x1, y1) is the coordinates of the number d1 in the packed layout, and (x2, y2) is the coordinates of number d2 . Coordinates are specified as integers with (0,0) denoting the lower-left corner of the packing area.
If multiple packings are possible, any packing meeting the criteria outlined above will be accepted.
输入样例
1 5 3 3 5 2 -1 0 0
输出样例
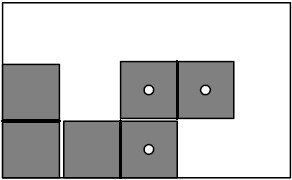
1 5 3 0 0 0 0 0 1 0 1 1 0 2 0 1 1 3 0 3 1 3 5 2 No packing is possible
提示
Note: This output corresponds to the packing shown here and is only one of many possible correct responses.

最后修改于 2020-10-29T06:44:55+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 1000 | 65536 |
登陆或注册以提交代码