当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
2793:Cactus
题目描述
Cactus is a connected undirected graph in which every edge lies on at most one simple cycle. Intuitively cactus is a generalization of a tree where some cycles are allowed. Your task first is to verify if the given graph is a cactus or not. Important difference between a cactus and a tree is that a cactus can have a number of spanning subgraphs that are also cactuses. The number of such subgraphs (including the graph itself) determines cactusness of a graph (this number is one for a cactus that is just a tree). The cactusness of a graph that is not a cactus is considered to be zero.
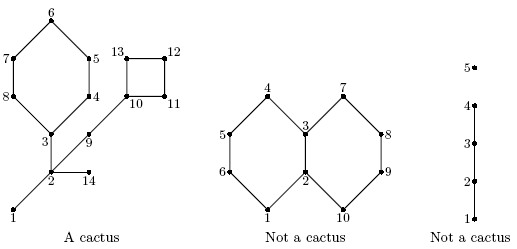
The first graph on the picture is a cactus with cactusness 35. The second graph is not a cactus because edge (2, 3) lies on two cycles. The third graph is not a cactus because it is not connected.

The first graph on the picture is a cactus with cactusness 35. The second graph is not a cactus because edge (2, 3) lies on two cycles. The third graph is not a cactus because it is not connected.
输入解释
The first line of the input contains two integer numbers n and m (1 <= n <= 20000, 0 <= m <= 1000).
Here n is the number of vertices in the graph. Vertices are numbered from 1 to n. Edges of the graphare represented by a set of edge-distinct paths, where m is the number of such paths.
Each of the following m lines contains a path in the graph. A path starts with an integer number ki(2 <= ki <= 1000) followed by ki integers from 1 to n. These ki integers represent vertices of a path. Path can go to the same vertex multiple times, but every edge is traversed exactly once in the whole input file.
There are no multiedges in the graph (there is at most one edge between any two vertices).
Here n is the number of vertices in the graph. Vertices are numbered from 1 to n. Edges of the graphare represented by a set of edge-distinct paths, where m is the number of such paths.
Each of the following m lines contains a path in the graph. A path starts with an integer number ki(2 <= ki <= 1000) followed by ki integers from 1 to n. These ki integers represent vertices of a path. Path can go to the same vertex multiple times, but every edge is traversed exactly once in the whole input file.
There are no multiedges in the graph (there is at most one edge between any two vertices).
输出解释
Write to the output a single integer number - the cactusness of the given graph. Note that cactusness can be quite a large number.
输入样例
14 3 9 1 2 3 4 5 6 7 8 3 7 2 9 10 11 12 13 10 2 2 14
输出样例
35
来自北京大学POJ的附加信息
| Case time limit(单组数据时间限制) | 2000MS |
最后修改于 2020-10-29T06:44:22+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 6000 | 65536 |
登陆或注册以提交代码