2401：Street Polygon

Two points p and q inside a simple polygon P are mutually visible, if the line segment connecting p and q does not include any point outside P. The points on the boundary edges of P are considered to be inside P. Two sets of points are said to be mutually weakly visible, if for each point in one set, there will be a point in the other set such that the two points are mutually visible. Given two distinct points s and t on the boundary of P, P is said to be a street polygon with respect to s and t, if the two boundary chains from s to t are mutually weakly visible. For example, the following figure shows a simple polygon which is a street and one which is not.

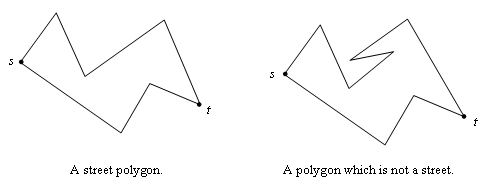
You are to write a program that given a simple polygon P with vertices v1, v2, ..., vn, determines if P is a street polygon with respect to vj and vk (which are two given distinct vertices of P).

The first line of the input contains a single integer t (1 <= t <= 10), the number of test cases, followed by the input data for each test case. The first line of each test case contains an integer n (3 <= n <= 20), the number of vertices of the simple polygon. Next, there are n lines, containing x and y coordinates of the vertex vi in the ith line, assuming there is an edge between vertices vi and vi+1, and also between vn and v1. x and y coordinates are assumed to be integers in the range 0 to 100. The last line of the test case contains two integers j and k (1 <= j, k <= n , j != k).

There should be one line in the output per test case containing a single word YES or NO, depending on whether P is a street with respect to vj and vk or not.