2364：Faucet Flow

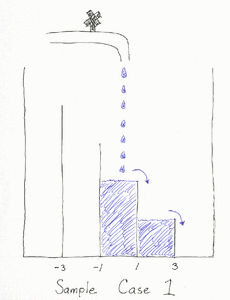A faucet is pouring water into a long, thin aquarium with various vertical dividers (walls) in it. The aquarium is initially empty, and its bottom is perfectly level. How long will it take for water to spill over its left- or right-most divider? The faucet is above location x=0, and the dividers are located at x=-1, -3, -5, ..., leftx and 1, 3, 5, ..., rightx. The dividers are attached perpendicular to the floor and sides of the aquarium, and have various heights. The aquarium's length is greater than rightx-leftx, its walls are higher than the highest divider, and its width is 1 unit everywhere. Water pours from the faucet at a rate of 1 cubic unit per second. [You may assume that water is an ideal liquid: it always flows downhill and if it cannot flow downhill it spreads at an equal rate in all horizontal directions.]

Each test case consists of two integers leftx (an odd number <= -1) and rightx (an odd number >= 1). Subsequent lines contain the height (a positive integer) of each divider from left to right. There will be no more than 1000 dividers in any test case. Input is terminated with a line containing two zeros.

For each case, output an integer on a single line, indicating how long it will take, in seconds, before water starts spilling over either the left or right divider.