当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
2285:The Floor Bricks
题目描述
Robert decided to decorate his new room with a cool pattern on the floor, composed with colorful floor bricks. After several days' work, he finally felt satisfied with the pattern he created with the odd shaped bricks. Soon, he found a problem. As the border of the pattern is not a perfect rectangle, the floor is not filled with bricks completely. However, since the shapes of the bricks are quite odd, it is not an easy work to fill the floor with these bricks completely. (Although a brick with a unit size is provided, this kind of brick is quite expensive usually. Fig.1 shows an example of a set of bricks) As Robert was very proud of his brick pattern, he refuses to modify even one brick in his pattern in order to satisfy the need of filling the floor completely. Instead, he asked you to find solutions for him to fill the rest part of the floor completely with the given bricks so that the Gils needed to buy these bricks are minimized. Of course, the bricks can not overlap each other to fill the floor. Please note that the bricks can be rotated, but cannot be flipped over. In addition, you may assume that all kinds of bricks can be contained within a 3×3 square box.
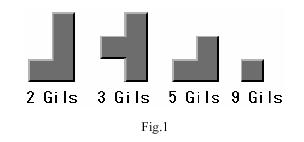
As the pattern of bricks covers most areas of the floor, the uncovered part of the floor is actually located at the bottom border of the rectangular shaped floor. Therefore, an uncovered part like the one in Fig.2 can be described with a series of integers, which represents the number of square blocks missed in each column, starting from the left. Thus, the shape in Fig.2 can be described with 11 integers: 2 2 1 2 3 5 2 3 3 4 1. In addition, you may assume that these integers are no larger than 5. Fig.3 shows a solution to fill the floor with the brick set in Fig.1 that costs minimal Gils.
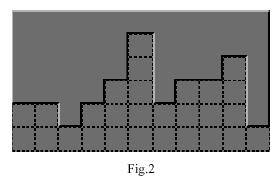
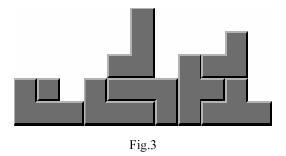
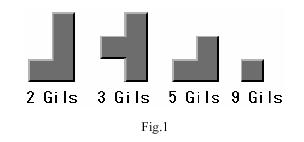
As the pattern of bricks covers most areas of the floor, the uncovered part of the floor is actually located at the bottom border of the rectangular shaped floor. Therefore, an uncovered part like the one in Fig.2 can be described with a series of integers, which represents the number of square blocks missed in each column, starting from the left. Thus, the shape in Fig.2 can be described with 11 integers: 2 2 1 2 3 5 2 3 3 4 1. In addition, you may assume that these integers are no larger than 5. Fig.3 shows a solution to fill the floor with the brick set in Fig.1 that costs minimal Gils.


输入解释
The input consists of at most 20 test cases. The first line of each test case contains an integer n ( 1<=n<=1000), which is the width of the floor. The second line contains n integers, separated by single spaces. These integers describe the shape of the uncovered floor as mentioned above. The third line contains an integer m ( 1<=m<=100), which is the number of bricks available. After this is the detailed description of the m bricks.
Each brick description consists of 4 lines. The first line is a positive integer, which is the price of that brick in Gils. After this line, there are three lines, each consisting of three characters, which describe the shape of the brick. A dot character represents a space in the shape and a sharp character # represents a square block in the shape. You can be sure that the blocks are always connected to form the brick.
There is a line containing a zero after the last test case, which signifies the end of the input and should not be processed.
Each brick description consists of 4 lines. The first line is a positive integer, which is the price of that brick in Gils. After this line, there are three lines, each consisting of three characters, which describe the shape of the brick. A dot character represents a space in the shape and a sharp character # represents a square block in the shape. You can be sure that the blocks are always connected to form the brick.
There is a line containing a zero after the last test case, which signifies the end of the input and should not be processed.
输出解释
For each test case, output a line `Need at least g Gil(s).', where g is the minimal Gils needed to fill the floor with the given bricks. If the floor cannot be filled with the given bricks, output `Impossible.' instead. Do not output blank lines between cases.
输入样例
11 1 4 3 3 2 5 3 2 1 2 2 4 2 #.. #.. ##. 3 .#. .## .#. 5 ... #.. ##. 9 ... .#. ... 1 1 1 1 ..# ... ... 1 1 1 1 .## ... ... 0
输出样例
Need at least 28 Gil(s). Need at least 1 Gil(s). Impossible.
最后修改于 2020-10-29T06:28:33+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 10000 | 65536 |
登陆或注册以提交代码