当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
2164:Find the Border
Special Judge 特殊评判题目描述
Closed polyline (with possible self-intersections) partitions a plane into a number of regions. One of the regions is unbounded -- it is an exterior of the polyline. All the bounded regions together with the polyline itself form an interior of the polyline (shaded in the picture below). The border of the interior (bold line in the picture) is a polyline as well. This polyline has the same interior as the original one.
Your task is to find the border of the interior of the given polyline.
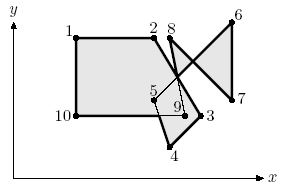
To guarantee the uniqueness (up to the starting point) of the polyline representing the border we require that the following conditions are satisfied for it:
Your task is to find the border of the interior of the given polyline.

To guarantee the uniqueness (up to the starting point) of the polyline representing the border we require that the following conditions are satisfied for it:
- it has no self-intersections, although may have self-touchings;
- no adjacent vertices of the border coincide;
- no adjacent edges of the border are collinear;
- when traversing the border, its interior is always to the left of its edges.
输入解释
The first line of the input file contains an integer number n (3 <= n <= 100) -- the number of vertices in the original polyline. Following n lines contain two integer numbers xi and yi on a line (0 <= xi, yi <= 100) -- coordinates of the vertices. All vertices are different and no vertex lies on an edge between two other vertices. Adjacent edges of the polyline are not collinear.
输出解释
Write to the output file an integer number m -- the number of vertices of the border. Then write m lines with coordinates of the vertices. Coordinates must be precise up to 4 digits after the decimal point.
输入样例
10 4 9 9 9 12 4 10 2 9 5 14 10 14 5 10 9 11 4 4 4
输出样例
13 9.3333 4 10 2 12 4 10.5 6.5 11.5 7.5 14 5 14 10 11.5 7.5 10 9 10.5 6.5 9 9 4 9 4 4
最后修改于 2020-10-29T06:25:14+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 1000 | 65536 |
登陆或注册以提交代码