当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
2163:Easy Trading
Special Judge 特殊评判题目描述
Frank is a professional stock trader for Advanced Commercial Markets Limited (ACM Ltd). He likes "easy trading" -- using a straightforward strategy to decide when to buy stock and when to sell it. Frank has a database of historical stock prices for each day. He uses two integer numbers m and n (1 <= m < n <= 100) as parameters of his trading strategy. Every day he computes two numbers: P(m) -- an average stock price for the previous m days, and P(n) — an average stock price for the previous n days. P(m) > P(n) is an indicator of the upward trend (traders call it bullish trend), and P(m) < P(n) is an indicator of the downward trend (traders call it bearish trend). In practice the values for P(m) and P(n) are never equal.
When a trend reverses from bearish to bullish it is a signal for Frank to buy stock. When a trend reverses from bullish to bearish it is a signal to sell.
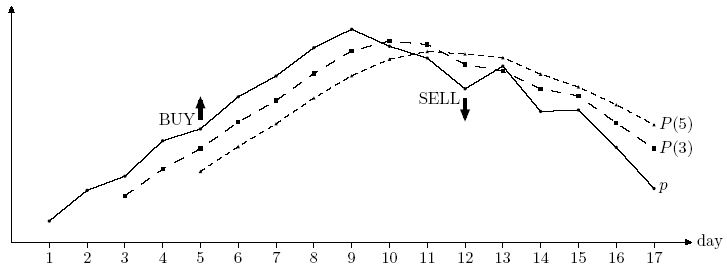
Frank has different values for m and n in mind and he wants to backtest them using historical prices. He takes a set of k (n < k <= 10 000) historical prices pi (0 < pi < 100 for 1 <= i <= k). For each i (n <= i <= k) he computes Pi(m) and Pi(n) — an arithmetic average of pi-m+1 . . . pi and pi-n+1 . . . pi respectively. Backtesting generates trading signals according to the following rules.
Your task is to write a program that backtests a specified strategy for Frank -- you shall print a signal for the first tested day (day n) followed by the signals in increasing day numbers.
When a trend reverses from bearish to bullish it is a signal for Frank to buy stock. When a trend reverses from bullish to bearish it is a signal to sell.

Frank has different values for m and n in mind and he wants to backtest them using historical prices. He takes a set of k (n < k <= 10 000) historical prices pi (0 < pi < 100 for 1 <= i <= k). For each i (n <= i <= k) he computes Pi(m) and Pi(n) — an arithmetic average of pi-m+1 . . . pi and pi-n+1 . . . pi respectively. Backtesting generates trading signals according to the following rules.
- If Pi(m) > Pi(n) there is a bullish trend for day i and a "BUY ON DAY i" signal is generated if i = n or there was a bearish trend on day i - 1.
- If Pi(m) < Pi(n) there is a bearish tread for day i and a "SELL ON DAY i" signal is generated if i = n or there was a bullish trend on day i - 1.
Your task is to write a program that backtests a specified strategy for Frank -- you shall print a signal for the first tested day (day n) followed by the signals in increasing day numbers.
输入解释
The first line of the input contains three integer numbers m, n, and k. It is followed by k lines with stock prices for days 1 to k. Each stock price pi is specified with two digits after decimal point. Prices in the input file are such that Pi(m) != Pi(n) for all i (n <= i <= k).
输出解释
Write to the output a list of signals -- one signal on a line, as described in the problem statement.
输入样例
3 5 17 8.45 9.10 9.40 10.15 10.40 11.08 11.52 12.12 12.51 12.15 11.90 11.25 11.73 10.77 10.80 10.01 9.14
输出样例
BUY ON DAY 5 SELL ON DAY 12
最后修改于 2020-10-29T06:25:12+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 1000 | 65536 |
登陆或注册以提交代码