当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
2108:Lazy Pianist
题目描述
Music and mathematics always had a close relationship. Since Pythagoras, it is known that tonal harmony is closely related to the numerical relation of the frequencies.
A lazy pianist, that uses to play VEERY LAARGE melodies composed by Kindermann, has taken advantage of this narrow relationship. However, this pianist commonly plays only the half or a quarter of the total notes. Amazingly, the audience never has realized his trick. The main reason is that this pianist always plays melodies that have a particular characteristic that is better described by the sequence of melody shown in figure 1.

Figure 1. A sequence generated by Kindermann
As you can see, the complete sequence is:
DO DO RE DO RE RE MI DO RE RE MI RE MI MI FA DO
However, if we choose only even notes, we can obtain the following sequence:
This is exactly the same melody. Even more, we can observe that choosing only every fourth note, we obtain:
DO DO RE …
And, this is exactly the same melody.
The lazy pianist would like to continue playing this kind of melodies, but he does not know how to complete the melody shown in figure 1. You must construct an algorithm in order to complete that melody.
A useful tip to do the job would be to assume that every note should be represented by an integer. Thus, DO=1, RE=2, MI=3, etc. Thus, sequence presented earlier could be seen as:

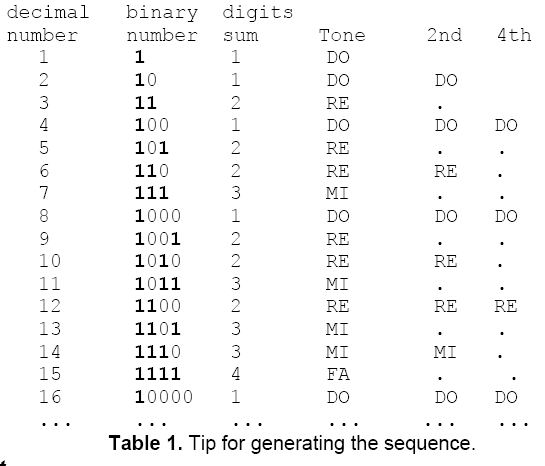
A possible algorithm for generating the sequence is shown in table 1. Every decimal number is expressed by its binary representation, and then we add the number of 1's that exist in that representation. This value indicates the note.
A lazy pianist, that uses to play VEERY LAARGE melodies composed by Kindermann, has taken advantage of this narrow relationship. However, this pianist commonly plays only the half or a quarter of the total notes. Amazingly, the audience never has realized his trick. The main reason is that this pianist always plays melodies that have a particular characteristic that is better described by the sequence of melody shown in figure 1.

Figure 1. A sequence generated by Kindermann
As you can see, the complete sequence is:
DO DO RE DO RE RE MI DO RE RE MI RE MI MI FA DO
However, if we choose only even notes, we can obtain the following sequence:
DO DO RE DO RE RE MI DO RE RE MI RE MI MI FA DO
DO DO RE DO RE RE MI DO
This is exactly the same melody. Even more, we can observe that choosing only every fourth note, we obtain:
DO DO RE …
And, this is exactly the same melody.
The lazy pianist would like to continue playing this kind of melodies, but he does not know how to complete the melody shown in figure 1. You must construct an algorithm in order to complete that melody.
A useful tip to do the job would be to assume that every note should be represented by an integer. Thus, DO=1, RE=2, MI=3, etc. Thus, sequence presented earlier could be seen as:

A possible algorithm for generating the sequence is shown in table 1. Every decimal number is expressed by its binary representation, and then we add the number of 1's that exist in that representation. This value indicates the note.

输入解释
Input consists of a list of three positive integers (total, cant, pos), preceded by an integer number that means the total of cases. Where total means total of tones to generate, cant means how many tones should be shown as a result, and pos means the start point. In this way, if cant=2, and pos=1, then this mean that it is needed to generate a sequence of 2 values starting from position number one. It is not allowed that pos has a value greater than total, and obviously neither that
((pos + cant ) -1) > total.
((pos + cant ) -1) > total.
输出解释
A sequence of positive integers separated by a space. Each integer means one note of the melody .
输入样例
5 16 3 10 2 2 1 5 5 2 8 1 8 15 15 1
输出样例
Case 1: 2 3 2 Case 2: 1 1 Case 3: It cannot be solved. Case 4: 1 Case 5: 1 1 2 1 2 2 3 1 2 2 3 2 3 3 4
最后修改于 2020-10-29T06:23:39+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 1000 | 30000 |
登陆或注册以提交代码