2053：Square

Given a square at [0, 1] * [0, 1] that has N points ( P₁, P₂, ..., P_N ) in the square (you may assume that different points can be at the same position), we can connect the N points and the four corners of the square with some line segments so that through these segments any two of the N+4 points can reach each other (directly or indirectly). The graph length is defined as the total length of the line segments. When N points' positions are fixed, there must exist a way of connecting them, such that it will make the shortest graph length. We can use LEN (P₁, P₂, ..., P_N) to record the graph length using this way of connecting.

In this situation, LEN (P₁, P₂, ..., P_N) is a function of P₁, P₂, ..., P_N. When P₁, P₂, ..., P_N change their positions, LEN (P₁, P₂, ..., P_N) also changes. It's easy to prove that there exist some P₁', P₂', ..., P_N' in the square such that LEN (P₁', P₂', ..., P_N') is at its minimum.

Given the initial positions of N points, your task is to find out N points P₁", P₂", ..., P_N" in the square such that |P₁P₁"| + |P₂P₂"| + ... + |P_NP_N"| is minimum and LEN (P₁", P₂", ..., P_N") = LEN (P₁', P₂', ..., P_N') . You are requested to output the value of |P₁P₁"| + |P₂P₂"| + ... + |P_NP_N"|, where |PiPi"| is the distance between Pi and Pi".

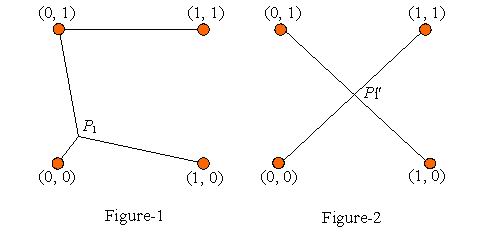
For example, Figure-1 gives the initial position of P₁ and the way of connecting to obtain LEN (P₁). In Figure-2, it gives the position of P₁", which is at the center of the square, and the way of connecting to obtain LEN (P₁"). It can be proved that LEN (P₁") = LEN (P₁’); your job is to output the distance between P₁ and P₁".

The input consists of several test cases. For each test case, the first line consists of one integer N (1 <= N <= 100), the number of points, and N lines follow to give the coordinates for every point in the following format:
x y

Here, x and y are float numbers within the value [0, 1].

A test case of N = 0 indicates the end of input, and should not be processed.

For each test case, output the value of |P₁P₁"| + |P₂P₂"| + ... + |P_NP_N"|. The value should be rounded to three digits after the decimal point.