1926：Pollution

The managers of a chemical plant, which is notorious for its high pollution, plan to adopt a newly developed device in order to reduce the amount of contaminants emitted. However, engineers in the plant are against this plan, as they doubt the usefulness of the device. As engineers only believe in experimental results, managers decide to hire programmers to make a numerical experiment to convince the engineers.

The new pollution-reducing device consists of several tanks with pipes connecting the tanks. You may assume there is at most one pipe between two tanks. Two tanks are called adjacent if a pipe connects them. When operating, the contaminant circulates in the device among these tanks.

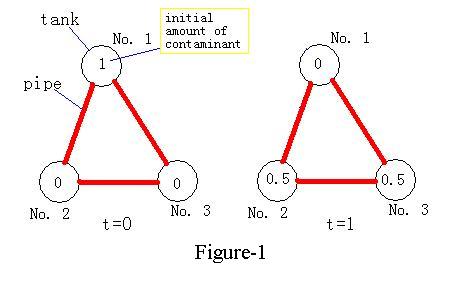
As shown in the Figure-1, the contaminant in one tank in time t, will equally distribute into all adjacent tanks in the time t+1. In other words, if we use X_i^t to denote the amount of contaminant in tank i at time t, we can use the following formula:

__poj_jax_start__X_i^{t+1}=\sum_j\frac{I_{ij}X_j^t}{d_j}__poj_jax_end__
where I_ij=1 if tank i and tank j are adjacent, otherwise I_ij=0, and where d_j is the number of tanks adjacent to tank j. If no tank is adjacent to tank i, we have X_i^t+1=X_i^t.
The managers, as well as the engineers, want to know that given the initial amount of contaminant in each tank, how the contaminant will be distributed in all the tanks after a long period of time in circulation. Namely, given X_i⁰ for all i, what are X_i^t when the difference between X_i^t and X_i^t+1 is so small that it can be ignored. You may assume that this condition will ALWAYS be attained from an initial case in this problem.

The first line of the input contains one integer T (1 <= T <= 10), the number of test cases. T cases then follow. For each test case, the first line consists of two integers: N and M where(1 <= N <= 100, 0 <= M <= N*(N-1)/2), is the number of tanks and pipes. The following N lines give the initial amount of contaminant for each tank, which are nonnegative real numbers and no larger than 100. Then the next M lines give the tanks that each pipe connects, as "A B" (1 <= A, B <= N, A != B) denotes there is a pipe between tank A and tank B.

For each test case, output the final amount of contaminant X_i^t+1 (one per line), followed by a blank line. The number should be rounded to three digits after the decimal point.