当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
1707:Sum of powers
题目描述
A young schoolboy would like to calculate the sum
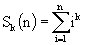
for some fixed natural k and different natural n. He observed that calculating ik for all i (1<=i<=n) and summing up results is a too slow way to do it, because the number of required arithmetical operations increases as n increases. Fortunately, there is another method which takes only a constant number of operations regardless of n. It is possible to show that the sum Sk(n) is equal to some polynomial of degree k+1 in the variable n with rational coefficients, i.e.,
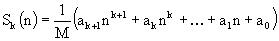
We require that integer M be positive and as small as possible. Under this condition the entire set of such numbers (i.e. M, ak+1, ak, ... , a1, a0) will be unique for the given k. You have to write a program to find such set of coefficients to help the schoolboy make his calculations quicker.
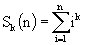
for some fixed natural k and different natural n. He observed that calculating ik for all i (1<=i<=n) and summing up results is a too slow way to do it, because the number of required arithmetical operations increases as n increases. Fortunately, there is another method which takes only a constant number of operations regardless of n. It is possible to show that the sum Sk(n) is equal to some polynomial of degree k+1 in the variable n with rational coefficients, i.e.,
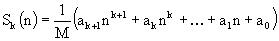
We require that integer M be positive and as small as possible. Under this condition the entire set of such numbers (i.e. M, ak+1, ak, ... , a1, a0) will be unique for the given k. You have to write a program to find such set of coefficients to help the schoolboy make his calculations quicker.
输入解释
The input file contains a single integer k (1<=k<=20).
输出解释
Write integer numbers M, ak+1, ak, ... , a1, a0 to the output file in the given order. Numbers should be separated by one space. Remember that you should write the answer with the smallest positive M possible.
输入样例
2
输出样例
6 2 3 1 0
最后修改于 2020-10-29T06:11:43+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 1000 | 10000 |
登陆或注册以提交代码