1697：The Erythea Campaign

O' mighty warrior,
Thy mission is to slay the foul king of Erythea.
Thou shall find him in his realm in the south.
God bless you,
King of Isladia.
After reading the order, you know you have a long, dangerous way down to the south, to find the king of Erythea in his realm and kill him. The Erythea realm is a rectangular region, with a number of horrible strongholds in it. Impenetrable walls enclose the region, so the only way for you to enter the realm is to fly by your Pegasus (flying horse) and land in some point in the region. The hiding place of the king is known so you just need to find your way to that location. As the area is extensive and covered by different terrain types, you have to travel on the grid-like roads in the region. The problem is, there are many guards on the towers of strongholds who can see you, and once seen, you have no chance to see your family again! The closer you travel to the strongholds, the greater the chances to be seen by the guards. The problem is to find the safest way from the point your Pegasus lands to the point where the king is.
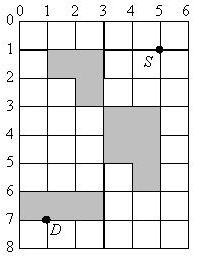
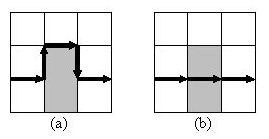
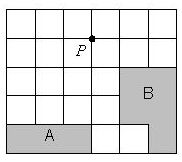
More abstractly, you have an m * n grid with squares of the same size, denoting the realm and the roads in it. You can travel along the lines in the grid (roads), and at each intersection (road crossing) you may turn into another road. Assume each stronghold comprises a set of adjacent squares of the grid (Figure 1). As you cannot enter a stronghold, your path never intersects the interior of a stronghold, yet you can travel on a road which is on stronghold boundaries (Figure 2). Suppose you can land your Pegasus exactly on a road crossing (the source point - S in Figure 1) and the hiding place of the king is on another road crossing (the destination point - D in Figure 1). Neither of these points lie inside a stronghold but may be placed on a stronghold boundary (as D does in Figure 1). Each road crossing is assigned a risk level which depends on the shortest road distance from the crossing to a point of the grid which is on the boundary of a stronghold. For a road crossing with the shortest road distance d to a boundary of strongholds, the risk level equals to m + n - d (Figure 3). It is assumed that there is at least one stronghold in the region, so that the definition of risk level is well-defined. The problem is, given the region's map and the source and destination points, find the path from the source to the destination which lies on the grid lines, so that sum of the risk levels of the points on the path (including source and destination) be minimum. As stated before, the path cannot intersect the interior of a stronghold.

Figure 1. An 8 * 6 region. You can travel along the grid lines (including boundary lines). The shaded squares are strongholds.	Figure 2. (a) Traveling on the boundary of a stronghold is allowed. (b) Crossing a stronghold is not allowed.	Figure 3. Point P in a 5*6 grid has distance 3 from stronghold A and distance 2 from stronghold B. Thus, risk level of P is (5+6)-2 = 9.

The input consists of several test cases. The first line of the file contains a single number M, which is the number of test cases in the file (1 <= M <= 10). The rest of the file consists of the data of the test cases. Each test case data begins with a line containing the number of rows and the number of columns in the grid, which are in the range 1 to 80. The second line of a test case contains two pairs of integers, which are y and x coordinates of the source point (where the Pegasus landed) and the y and x coordinates of the destination point (where you may find the king). The horizontal and vertical lines in the grid are indexed from left to right and top to bottom from 0, so the coordinates can be expressed using these indices.
Following the first two lines, there are lines that describe the map of the region. Each line consists of a string of 0's and 1's, describing squares of the corresponding row. A 1 in the string tells you that the corresponding square in the grid belongs to a stronghold. The width of the region is the length of all strings, and its height in the number of strings.

The output for each test case is the total risk of the minimum risk path from the landing point to the destination. Recall that the total risk of a path is sum of the risk levels of the points in the path (including source and destination). If no path exists between source and destination, the output should be 'no solution'. The output for each test case must be written on a separate line.

The above input file contains two test cases. The first test case is the one shown in Figure 1.