1682：Clans on the Three Gorges

On the banks of the Three Gorges of the Yangtze River live some old clans. For historical reasons, clans on the same gorge hate each other, and conflicts often arise between them for lands and recourses. On the contrary they have a long and deep friendship with the clans on the other gorges. But it's difficult for them to travel to the other sides of the gorge because of the torrent flow of the Yangtze River.

One day they decide to build suspension bridges between the gorges. The gorges have three banks (figure 1), and each bank is rolling so clans have different altitude. Every clan will not share a same bridge with other clans on the same bank, so there must be at least one bridge for each clan. And for safety reason, bridges are not allowed to cross each other overhead, or if a bridge collapsed, it would fall on another one. Experts point out that if the altitudes of the two ends of a bridge are different, the bridge will be troublesome to build and cost more. It's estimated that the cost of a bridge is equal to the fall of the ends of the bridge. The clans are not rich, so they employ you to find a solution to minimize the cost to build the suspension bridges to satisfy their demand.

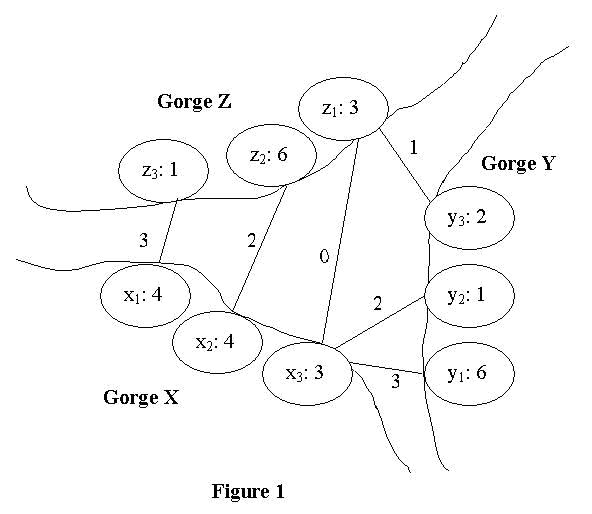
As show in figure 1, the three gorges are named X, Y and Z respectively. A clan is represented by a cycle, with its name and altitude in. Clans on gorge X are named x1, x2... xn in counter-clockwise order. Those on gorge Y and gorge Z are y1, y2... ym and z1, z2? zk in counter-clockwise order too. A bridge is represented by a line between two clans with its cost on it. No two lines can intersect and no clan has zero degree according to the description of this problem.

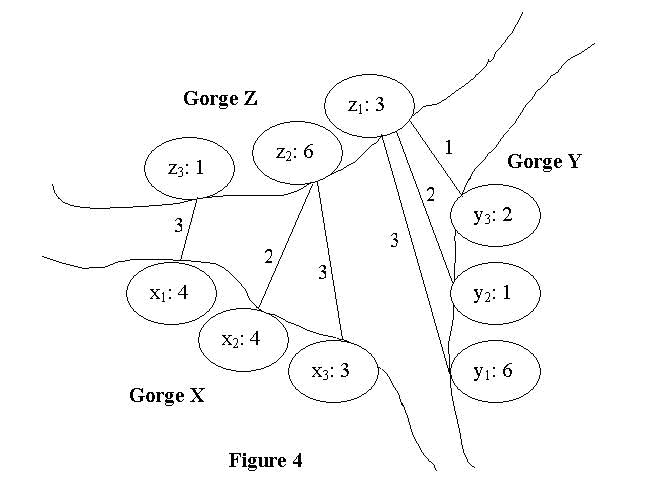
For example, figure 2 is invalid solution because the two bridges intersect. Figure 3 is also invalid for the reason that clan y1 doesn't has a bridge for its own. Figure 1 and Figure 4 both are valid solutions for there are no intersected bridges or isolated clan in these solutions. The cost of a solution is the sum of all the costs of the bridges in the solution. And the cost of a bridge is equal to the absolute value of the difference of the heights of the two ends. So figure 1 has cost 11 against 14 of figure 4. It's clear that figure 1 is a better solution. In fact, it's one of the best solutions. You are required to write a program to find the minimum cost.

The input consists of T test cases. The first line contains the number T (1 <= T <= 10). Then follow the T test cases. Each test case is started with a line contains three integers n, m and k (1 <= n, m, k <= 100), representing the number of clans on gorges X, gorge Y and gorge Z. The next three lines will contain the height of clans on the three gorges, the heights are positive integer less than 100. Test cases are separated by a blank line. The clans are named as described in the comment of figure 1. Their names also refer to their altitude. So the input of a case is of the form:

n m k
x1 x2 x3 ... xn
y1 y2 y3 ... ym
z1 z2 z3 ... zk

The output contains T integers. Each line contains the minimum cost to the corresponding case of the input.