1670：Obstructed Rook Circuits

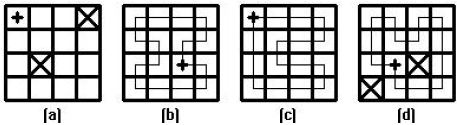
A board is a rectangular array of squares such as on a chessboard, with possibly some squares blocked off. A rook tour of a board is a path that visits each empty square of the board exactly once, moving at each step to an empty adjacent square (North, South, East or West but not diagonally). A rook tour is a rook circuit if it starts and ends on the same square. In the figures below, let the + symbol be the rook, and the X symbol be an obstruction. The following are descriptions of each figure: (a) is a board with no rook circuit, (b) and (c) give distinct rook circuits of the same board and (d) gives the unique (up to direction) rook circuit of another board.

Write a program, which takes as input the description of a board and either finds a rook circuit or determines that there is no rook circuit.

Input consists of a sequence of board descriptions and starting points. The first line of the input is
Nrows Ncols Nblocks StartX StartY
where Nrows is the number of rows in the rectangular array, Ncols is the number of columns in the rectangular array, Nblocks is the number of blocked off squares on the board and (StartX, StartY) is the position on the board where the path is to start (and end). StartX and StartY are 0 based (StartX ranges from 0 to Ncols - 1). Following the first line there are Nblocks lines giving the coordinates of the blocked off squares, one per line. The coordinates of these points are 0 based and are of the form X Y. The final line of each board description is a blank line.
The last line of the input is line of 5 zeroes.

If there is no rook circuit for the corresponding board, the output is a line "NO SOLUTION" followed by a blank line. Otherwise, the output is a sequence of the letters N, S, E, W giving the moves from the starting point to traverse a rook circuit and return to the starting point. (N indicates moving to the previous row, S moving to the next row, E moving to the next column and W moving to the previous column.) If more than 40 moves are required, the moves will be output 40 to a line (except possibly for the last line). The move output is to be followed by a blank line.
Note that the same board may
have several rook circuits. Your program need only find any one (correct) rook circuit.

Some Facts:
1. The Parity Principle. If we checker the squares of the array black and white (white if (x+y) is even, black if (x+y) is odd), each unit step in a rook circuit must go from a white square to a black square and vice versa.Thus any rook circuit must have the same number of white and black squares. Board (a) above has 8 white and 6 black unblocked squares so cannot have a rook circuit.
2. The Two Neighbor Principle. If a square has only two neighbors, then it must be visited via those neighbors. When a circuit gets to one of the neighbors, it must pass next to the two -neighbor square and then to the other neighbor. In board (d), the (0,0), (3, 0), (0, 2), (1,3), (2,3), (3,3) and (3,2) squares each have two neighbors. Thus the path is forced to include (1,0)-(0,0)-(0,1)-(0,2)-(1,2)-(1,3)-(2,3)-(3,3)-(3,2)-(3,1)-(3,0)-(2,0) in either order.
3. The Cul-de-Sac Principle. Never draw segments that leave a square with only one exit.
4. The Early Closing Principle. Never close a circuit until all squares have been visited.