当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
1452:Signal Box
题目描述
Background
On its trip, a train has to pass a lot of points (American English: switches) and signals. The train抯 track depends on the status of points and signals. The responsible operator on the signal box does not handle them separately, but tells the signal box the start and destination signal of the train抯 journey. The box then determines the correct status of points and signals and brings them into the right position.
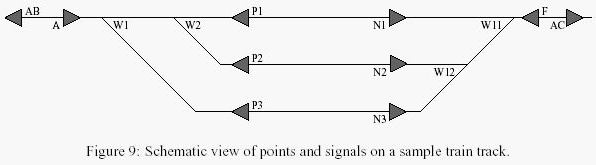
Figure 9 shows a sample scenario in which railway tracks are shown as solid lines and signals are drawn as triangles (this is also the first scenario of the sample input). Signals have a sense of direction: they are only valid for the direction in which the triangle points (e.g., signal A is valid for trains running from left to right, see also Figure 10). Points are located where railway tracks meet (e.g., at points W1, W2, etc.). Points have a front side (i.e., the side from which a train can take alternative directions) and a back side and can be in two positions, named + and -. If a train comes from the front side, it leaves the point at the + or - leg, dependent on the point抯 position (see Figure 11). If the train comes from one of the the back legs, it leaves it at the front leg. Even then the point has to be put into the right state, otherwise it gets damaged!

Problem
Your task is to implement an automatic signal box, i.e., write a program which finds the correct position of points and signals for a given start and destination. The signal box should follow these rules:
A journey can only start and end at a signal. Both signals have to be in the same direction!
During a journey a train must not change its direction.
The journey consists of a sequence of signal and point settings. A signal is only taken into account for the journey if it has the right direction. A point along the way is always taken into account.
If there is more than one possible track from the start signal to the destination signal, the correct one is determined by the following scheme:
Consider a set of path selection rules. These are given as a triple (x, y, z) of point identifiers x and y, and a position z. A selection rule has the following meaning:
If there are alternative paths starting at point x and ending at point y where x is approached from the front and y from the back, then consider only paths in which x is in position z (z is either + or -).
If no such rule exists for a given point x, the - position must be chosen.
The sample in- and output demonstrate the application of the rules. Furthermore, you can make the following assumptions:
The track plan is acyclic.
Within a path, each element is only used once or not at all.
If for a given point x several rules (x, y, z) exist, they will agree on the position to be chosen.
On its trip, a train has to pass a lot of points (American English: switches) and signals. The train抯 track depends on the status of points and signals. The responsible operator on the signal box does not handle them separately, but tells the signal box the start and destination signal of the train抯 journey. The box then determines the correct status of points and signals and brings them into the right position.

Figure 9 shows a sample scenario in which railway tracks are shown as solid lines and signals are drawn as triangles (this is also the first scenario of the sample input). Signals have a sense of direction: they are only valid for the direction in which the triangle points (e.g., signal A is valid for trains running from left to right, see also Figure 10). Points are located where railway tracks meet (e.g., at points W1, W2, etc.). Points have a front side (i.e., the side from which a train can take alternative directions) and a back side and can be in two positions, named + and -. If a train comes from the front side, it leaves the point at the + or - leg, dependent on the point抯 position (see Figure 11). If the train comes from one of the the back legs, it leaves it at the front leg. Even then the point has to be put into the right state, otherwise it gets damaged!

Problem
Your task is to implement an automatic signal box, i.e., write a program which finds the correct position of points and signals for a given start and destination. The signal box should follow these rules:
A journey can only start and end at a signal. Both signals have to be in the same direction!
During a journey a train must not change its direction.
The journey consists of a sequence of signal and point settings. A signal is only taken into account for the journey if it has the right direction. A point along the way is always taken into account.
If there is more than one possible track from the start signal to the destination signal, the correct one is determined by the following scheme:
Consider a set of path selection rules. These are given as a triple (x, y, z) of point identifiers x and y, and a position z. A selection rule has the following meaning:
If there are alternative paths starting at point x and ending at point y where x is approached from the front and y from the back, then consider only paths in which x is in position z (z is either + or -).
If no such rule exists for a given point x, the - position must be chosen.
The sample in- and output demonstrate the application of the rules. Furthermore, you can make the following assumptions:
The track plan is acyclic.
Within a path, each element is only used once or not at all.
If for a given point x several rules (x, y, z) exist, they will agree on the position to be chosen.
输入解释
The first line contains the number of scenarios.
In the first line of the input for every scenario, you are given two signal identifiers for the departure and the destination, separated by a single blank. The following line contains the number n of elements (points and signals) in the track plan. You can assume 1<=n<=200 and that each element has a unique identifier of at most 20 alphanumeric characters. The identifier "XXX" is given to track ends.
There are signal and point elements, given in the following format:
Points are specified by a line "W I F M P" where W stands for "Weiche" (German for point), I is the identifier of the point, F identifies the front element of the point, and M and P give the identifiers of the back elements of the point depending on whether it is in minus or plus position.
Signals are specified by a line "S I F B" where S stands for "Signal" (German for signal), I is the identifier of the signal, and F and B give the identifiers of the front and back elements of the signal.
The direction for which the signal is valid is from front to back.
The following line contains the number p, 0<=p<=100, of path selection rules, followed by another p lines of the rules themselves. A rule is of the form "FW X Y Z" where FW is the identifier of "Fahrstrabenwahl-Regel" (German for path selection rule), X, Y and Z are the elements of the rule as explained above.
In the first line of the input for every scenario, you are given two signal identifiers for the departure and the destination, separated by a single blank. The following line contains the number n of elements (points and signals) in the track plan. You can assume 1<=n<=200 and that each element has a unique identifier of at most 20 alphanumeric characters. The identifier "XXX" is given to track ends.
There are signal and point elements, given in the following format:
Points are specified by a line "W I F M P" where W stands for "Weiche" (German for point), I is the identifier of the point, F identifies the front element of the point, and M and P give the identifiers of the back elements of the point depending on whether it is in minus or plus position.
Signals are specified by a line "S I F B" where S stands for "Signal" (German for signal), I is the identifier of the signal, and F and B give the identifiers of the front and back elements of the signal.
The direction for which the signal is valid is from front to back.
The following line contains the number p, 0<=p<=100, of path selection rules, followed by another p lines of the rules themselves. A rule is of the form "FW X Y Z" where FW is the identifier of "Fahrstrabenwahl-Regel" (German for path selection rule), X, Y and Z are the elements of the rule as explained above.
输出解释
The output for every scenario begins with a line containing "Scenario #i:", where i is the number of the scenario starting at 1.
For every scenario print out the elements on the path from departure to destination in the order they are passed by the train. However, print the signals first, followed by the points. Every element of the path must be on a line by itself. Elements of the path are signal and point identifiers (the first and the last signal identifiers must also be printed). For every point you should also give the correct position of the point as either + or - on the same line, separated from the point identifier by a single blank. If there is no possible path, print "NOT POSSIBLE".
Terminate each scenario by a blank line.
For every scenario print out the elements on the path from departure to destination in the order they are passed by the train. However, print the signals first, followed by the points. Every element of the path must be on a line by itself. Elements of the path are signal and point identifiers (the first and the last signal identifiers must also be printed). For every point you should also give the correct position of the point as either + or - on the same line, separated from the point identifier by a single blank. If there is no possible path, print "NOT POSSIBLE".
Terminate each scenario by a blank line.
输入样例
4 A AC 14 S AB A XXX S A AB W1 W W1 A W2 P3 W W2 W1 P1 P2 S P1 N1 W2 S N1 P1 W11 W W11 F N1 W12 S F AC W11 S AC F XXX S P2 N2 W2 S N2 P2 W12 W W12 W11 N3 N2 S P3 N3 W1 S N3 P3 W12 2 FW W1 W11 + FW W11 W1 - S1 S2 2 S S1 S2 XXX S S2 S1 XXX 0 S1 S4 6 S S1 XXX W1 S S2 W1 XXX S S3 XXX W2 S S4 W2 XXX W W1 S1 S2 W2 W W2 S4 W1 S3 0 S1 S2 8 S S1 XXX W1 S S2 W4 XXX S S3 W1 W2 S S4 W3 W4 W W1 S1 W2 S3 W W2 W3 W1 S3 W W3 W2 W4 S4 W W4 S2 W3 S4 1 FW W1 W2 +
输出样例
Scenario #1: A N3 AC W1 + W12 - W11 + Scenario #2: NOT POSSIBLE Scenario #3: S1 S4 W1 + W2 - Scenario #4: S1 S3 S2 W1 + W2 + W3 - W4 -
最后修改于 2020-10-29T06:04:36+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 1000 | 10000 |
登陆或注册以提交代码