当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
1393:Fold-up Patterns
题目描述
Fold-up patterns for solids like cubes or octahedrons can be found in many books on geometry, but without actually folding them it is hard to tell whether the constructions really work. In this problem, we will consider a special class of such patterns.
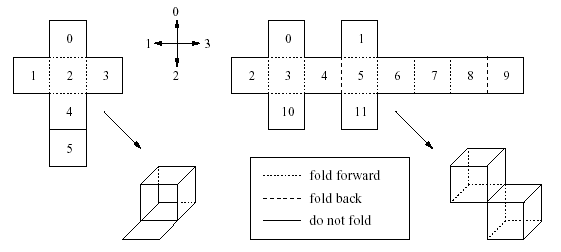
Given a fold-up pattern built from unit squares in the plane, together with a description along what edges it should be folded in what direction, decide whether it will result in a closed surface of a solid in three dimensions. If it does, find the volume of the solid.
More precisely, the pattern consists of a connected set of unit squares in the plane. For any edge between connected sides you are told whether to fold forward, backward (always at a right angle), or not at all along that edge. If an edge between two adjacent squares in the pattern is not mentioned in the input, you may assume that the squares are not connected and can be ripped apart when folding. However, connected edges must always be folded according to the description.
For our purposes a closed surface is one where every square in the pattern separates the inside from the outside. When folded, the squares of the pattern lie on a rectangular, 3-dimensional grid, and each separates a cell (cubes of side length one unit) on the inside from one on the outside. For every cell it must be clear whether it is inside or outside. The following sketch illustrates this rule in two dimensions.
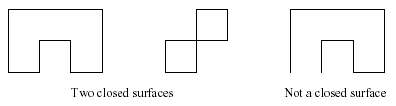
Note that even the second pattern above satisfies our definition of a closed surface, but the interior is not connected.
Two different squares may not occupy exactly the same position in space, though they may (and will for a closed surface) touch at edges and vertices. Make sure that the pattern does not interpenetrate itself through connected edges. Apart from that, do not worry about the process of folding, e.g. what edges are folded first or whether part of the structure is in the way for the rest.

Given a fold-up pattern built from unit squares in the plane, together with a description along what edges it should be folded in what direction, decide whether it will result in a closed surface of a solid in three dimensions. If it does, find the volume of the solid.
More precisely, the pattern consists of a connected set of unit squares in the plane. For any edge between connected sides you are told whether to fold forward, backward (always at a right angle), or not at all along that edge. If an edge between two adjacent squares in the pattern is not mentioned in the input, you may assume that the squares are not connected and can be ripped apart when folding. However, connected edges must always be folded according to the description.
For our purposes a closed surface is one where every square in the pattern separates the inside from the outside. When folded, the squares of the pattern lie on a rectangular, 3-dimensional grid, and each separates a cell (cubes of side length one unit) on the inside from one on the outside. For every cell it must be clear whether it is inside or outside. The following sketch illustrates this rule in two dimensions.
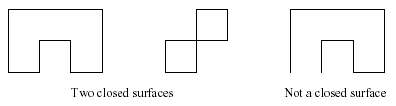
Note that even the second pattern above satisfies our definition of a closed surface, but the interior is not connected.
Two different squares may not occupy exactly the same position in space, though they may (and will for a closed surface) touch at edges and vertices. Make sure that the pattern does not interpenetrate itself through connected edges. Apart from that, do not worry about the process of folding, e.g. what edges are folded first or whether part of the structure is in the way for the rest.
输入解释
The input file consists of several test cases.
For each test case, the first line contains two integers n and e. These are the number n (1 <= n <= 200) of squares in the pattern and the number e (0 <= e <= 300) of edges. Squares are labelled by the integers 0 to n - 1. The following e lines describe one edge each using the four numbers s1; s2; p; f :
The two numbers s1 and s2 (with 0 <= s1 < s2 < n) of the squares that are joined by the edge.
The position p of the square s2 with respect to the square s1 in the pattern. Here p = 0;1;2;3 mean above, to the left, below, or to the right of s1, respectively (see sketch below).
The number f =0;1;2 tells you to fold along the edge either not at all, forward, or back, respectively (see sketch).
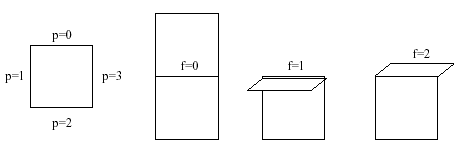
You can also assume that the pattern is connected and can be drawn in the plane without overlapping.
At the end of the input file, there will be a line containing two zeros (instead of n and e). Do not process that line.
For each test case, the first line contains two integers n and e. These are the number n (1 <= n <= 200) of squares in the pattern and the number e (0 <= e <= 300) of edges. Squares are labelled by the integers 0 to n - 1. The following e lines describe one edge each using the four numbers s1; s2; p; f :
The two numbers s1 and s2 (with 0 <= s1 < s2 < n) of the squares that are joined by the edge.
The position p of the square s2 with respect to the square s1 in the pattern. Here p = 0;1;2;3 mean above, to the left, below, or to the right of s1, respectively (see sketch below).
The number f =0;1;2 tells you to fold along the edge either not at all, forward, or back, respectively (see sketch).

You can also assume that the pattern is connected and can be drawn in the plane without overlapping.
At the end of the input file, there will be a line containing two zeros (instead of n and e). Do not process that line.
输出解释
For each scenario print "Test case #k:", where k is the number of the test case (starting from 1).
Then, on the same line, print either "not a closed surface" if the pattern does not form a closed surface or "closed surface, volume=" and the volume as an integer if it does.
Then, on the same line, print either "not a closed surface" if the pattern does not form a closed surface or "closed surface, volume=" and the volume as an integer if it does.
输入样例
6 5 0 2 2 1 1 2 3 1 2 3 3 1 2 4 2 1 4 5 2 1 5 4 0 2 2 1 1 2 3 1 2 3 3 1 2 4 2 1 0 0
输出样例
Test case #1: closed surface, volume=1 Test case #2: not a closed surface
提示
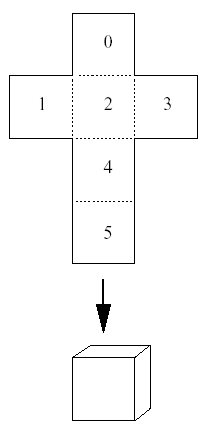
最后修改于 2020-10-29T06:02:49+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 5000 | 30000 |
登陆或注册以提交代码