1353：Color Change of Go Game Pieces

Assume that there are lots of two colors of black and white Go Game Pieces in a box, we take out n Go Game Pieces (0 < n < 129, n is a natural number) each time from the box, among which all the m pieces taken out earlier are white and the latter pieces are all black. Place all pieces around a circle in sequence uniformly. Thereafter according to the distributing of color of these pieces of this circle, taking out other pieces from this box and placing another circle in sequence uniformly, namely putting a new piece between two piece from head to end of this circle, put a black piece between every two white pieces; put a white between every white and black pieces; put a black between every two black pieces; put a white between every black and white pieces. In such way, there are also n pieces in the new circle. After that the original pieces are all taken off. Then repeat the above process. Doing in such way, that the original set of the pieces on the circle is taken away as soon as new set of the pieces has being placed on, how many white pieces are on the circle after the k-th time of repetition (k is a natural number, k < 10001)?

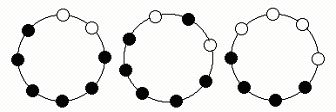
For example, when n=8, m=2, k=2, the situation is as following:

    Original    first repetition  second repetition

On every line a group of data is given. In each group there are three natural number n, m, k, separated by commas. After all data are given there is -1 as the symbol of termination.

Find the number of white pieces corresponding to the input data of each group. One line is for every output. Its fore part is a repetition of the input data and then it follows a colon and a space. The last part of it is the computed number of the white pieces.