1343：Rooted Trees Isomorphism

Isomorphism is the problem of testing whether two graphs are really the same. Suppose we are given a collection of graphs and must perform some operation on each of them. If we can identify which of the graphs are duplicate, they can be discarded so as to avoid redundant work.
First we have to explain what is meant when we say two graphs are the same. Two labeled graphs G1 = (V1,E2) and G2 = (V2,E2) are identical when we can find a mapping f of the vertices of G1 to the vertices of G2 such that (x, y) is an edge of G1 if and only if (f(x), f(y)) is an edge of G2. Such a mapping is called an isomorphism.
No efficient algorithm is known for the general graph isomorphism problem, but the problem is easier to determine whether two trees are isomorphic to each other. In Figure 7, it is not hard to verify that tree T1 is isomorphic to tree T3, but T1 is not isomorphic to T2.

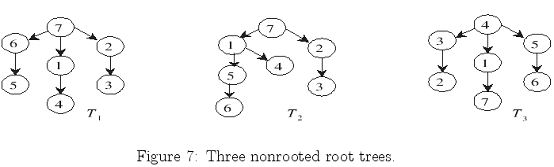
You are given a collection of k trees C = {T1, T2, ... , Tk} such that each Ti has exactly n nodes. The objective of the problem is to partition these trees into isomorphic (equivalent) classes such that any two trees within the same isomorphic class are isomorphic to each other.
A naive method of enumerating all possible mapping functions would require generating all possible n! different mappings. What resulted is a very time-consuming O(n!) time algorithm just to test two trees. You need to figure out a somehow clever way for solving the problem.

A collection of k (n-node) trees C = {T1, T2, ... , Tk}. The inputs are just a list of integers. The first 2 integers (in a single line) represent the number of trees, k, and the size of each tree, n. Note that k can be as large as 150 and n can be as large as 100. After the two integers, there will be k lines representing the edge sets for each tree Ti; each line contains exactly n-1 pairs of integers, representing the n-1 (directed) edges of each tree. Thus, there are totally 2n-2 integers for each tree, and the total input will be 2k(n-1) integers except the first two parameters. Each tree is indexed by their appearance ordering; that is, the first line represents the tree T1, the second line is T2, ... , etc, and the last (kth) line is just Tk.

For the given collection of trees, partition these trees into isomorphic (equivalent) classes such that any two trees within the same isomorphic class are isomorphic to each other. For each isomorphic class, output the indices of these isomorphic trees in a line. Suppose that there are m isomorphic classes, you need to print out m lines. For example, a line
t1 = t2 = ... = tp;
represents an isomorphic class of size p such that two trees Tti and Ttj , 1<=i, j <=p, are isomorphic to each other. For each line, output indices of those isomorphic trees in increasing order; that is, t1 < t2 < ... < tp. Further, print out these m isomorphic classes by their increasing lexical ordering; that is, by the ordering of their first indices. For example, suppose that there are 4 isomorphic classes {4, 2, 7}, {5, 1, 3}, {8, 9}, {6}. The output shall be
1 = 3 = 5 ;
2 = 4 = 7 ;
6 ;
8 = 9 ;