1246：Hilbert Curve Intersections

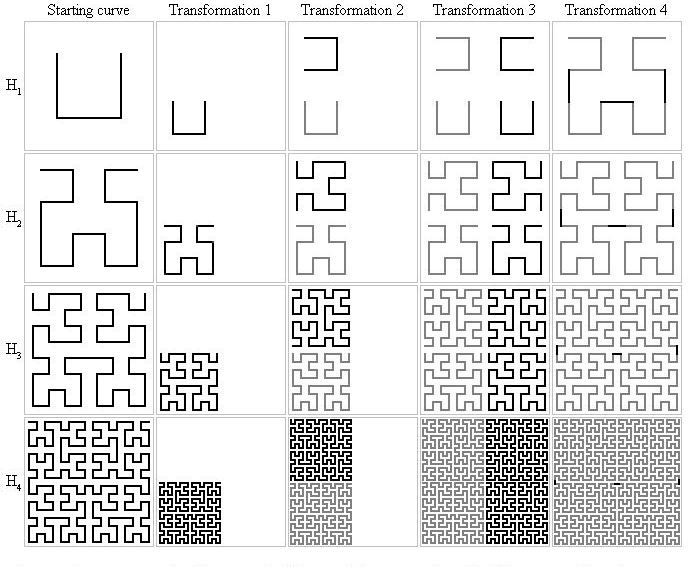
David Hilbert proved the existence of a very counter-intuitive curve that fills space. The construction of the Hilbert curve is based on a sequence of curves, H1, H2, H3, H4, ... composed of horizontal and vertical segments. Each curve lies in the unit square [0, 1] * [0, 1]. H1 contains just three segments, connecting the points (1/4, 3/4) to (1/4, 1/4) to (3/4, 1/4) to (3/4, 3/4). H_n is defined recursively in terms of H_n-1, for n = 2, 3, ... by four transformations:

1.Halve all coordinates in H_n-1.
2.Add a copy rotated 90 degrees counterclockwise about the point (0, 1/2).
3.Add the reflection across the line x = 1/2.
4.Let m = 1/2ⁿ⁺¹. Add segments connecting endpoints (1/2 - m, 1/2 - m) to (1/2 + m, 1/2 - m), (m, 1/2 - m) to (m, 1/2 + m), and (1 - m, 1/2 - m) to (1 - m, 1/2 + m).
Your job is to count the number of intersections of horizontal line segments with these curves. For example, consider Figures 1 and 2, which illustrate the first two example input data sets below.

The coordinates of vertices of Hn are odd multiples of 1/2ⁿ⁺¹. The coordinates of horizontal segment endpoints will always be multiples of 1/2ⁿ. Hence the specified horizontal segment can only cross vertical segments in H_n.

Input consists of one to 100 data sets, one per line, followed by a final line containing only 0. Each data set consists of four integers separated by blanks in the form
n x1 x2 y
which represents H_n and the segment from (x1/2ⁿ, y/2ⁿ) to (x2/2ⁿ, y/2ⁿ), where 0 < n < 31, x1 < x2, and each of x1, x2, and y lie in the range 0 to 2ⁿ, inclusive.

The output is one integer per line for each data set: the number of intersections of H_n with the segment. Caution: A brute force solution that computes each intersection individually will not finish within the one minute time limit. As you can see below, there may be more than one billion intersections for any data set.